题目内容
设不等式-2<|x-1|-|x+2|<0的解集为M,a、b∈M,
(1)证明:|
a+
b|<
;
(2)比较|1-4ab|与2|a-b|的大小,并说明理由.
(1)证明:|
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 4 |
(2)比较|1-4ab|与2|a-b|的大小,并说明理由.
考点:不等式的证明,绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)利用绝对值不等式的解法求出集合M,利用绝对值三角不等式直接证明:|
a+
b|<
;
(2)利用(1)的结果,说明ab的范围,比较|1-4ab|与2|a-b|两个数的平方差的大小,即可得到结果.
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 4 |
(2)利用(1)的结果,说明ab的范围,比较|1-4ab|与2|a-b|两个数的平方差的大小,即可得到结果.
解答:
解:(1)记f(x)=|x-1|-|x+2|=
由-2<-2x-1<0解得-
<x<
,则M=(-
,
).…(3分)
∵a、b∈M,∴|a|<
,|b|<
所以|
a+
b|≤
|a|+
|b|<
×
+
×
=
.…(6分)
(2)由(1)得a2<
,b2<
.
因为|1-4ab|2-4|a-b|2=(1-8ab+16a2b2)-4(a2-2ab+b2)
=(4a2-1)(4b2-1)>0,…(9分)
所以|1-4ab|2>4|a-b|2,故|1-4ab|>2|a-b|.…(10分)
|
由-2<-2x-1<0解得-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵a、b∈M,∴|a|<
| 1 |
| 2 |
| 1 |
| 2 |
所以|
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)由(1)得a2<
| 1 |
| 4 |
| 1 |
| 4 |
因为|1-4ab|2-4|a-b|2=(1-8ab+16a2b2)-4(a2-2ab+b2)
=(4a2-1)(4b2-1)>0,…(9分)
所以|1-4ab|2>4|a-b|2,故|1-4ab|>2|a-b|.…(10分)
点评:本题考查不等式的证明,绝对值不等式的解法,考查计算能力.

练习册系列答案
相关题目
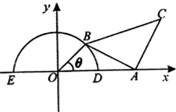 如图,半圆的圆心在直角坐标原点,点A,D,E的坐标分别为A(2,0),D(1,0),E(-1,0),且点B在半圆上自点D逆时针向点E运动,三角形ABC是等腰直角三形,∠BAC是直角,则四边形OACB的面积的最大值是( )
如图,半圆的圆心在直角坐标原点,点A,D,E的坐标分别为A(2,0),D(1,0),E(-1,0),且点B在半圆上自点D逆时针向点E运动,三角形ABC是等腰直角三形,∠BAC是直角,则四边形OACB的面积的最大值是( )A、
| ||||
B、2+2
| ||||
C、
| ||||
D、2+
|
若α∈(0,
),β∈(0,π)且tan(a-β)=
,tanβ=-
,则2α-β( )
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 7 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
已知平面向量
,
满足|
|=1,|
|=2,且(
-
)⊥
,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知复数z=
,则|z|=( )
| 5 |
| 1+2i |
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、5 |
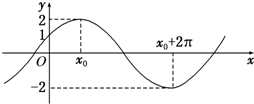 如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<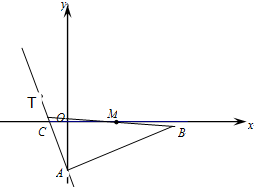 如图,在Rt△ABC中,∠A为直角,AB边所在直线的方程为x-3y-6=0,点T(-1,1)在直线AC上,斜边中点为M(2,0).
如图,在Rt△ABC中,∠A为直角,AB边所在直线的方程为x-3y-6=0,点T(-1,1)在直线AC上,斜边中点为M(2,0).