题目内容
向量
=（k，
），
=（2，-2）且
•
=-4
，则k的值为（ ）
| a |
| 2 |
| b |
| a |
| b |
| 2 |
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
考点：平面向量数量积的运算,平面向量的坐标运算
专题：平面向量及应用
分析：通过向量的数量积得到关系式，求出k即可．
解答：
解：向量
=（k，
），
=（2，-2）且
•
=-4
，
∴2k-2
=-4
，∴k=-
．
故选：D．
| a |
| 2 |
| b |
| a |
| b |
| 2 |
∴2k-2
| 2 |
| 2 |
| 2 |
故选：D．
点评：本题考查平面向量数量积的运算，平面向量的坐标运算，基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
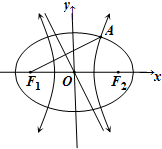如图，F1，F2是椭圆C1：| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 | ||
|
| 1 | ||
|
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
由0，1，2，3这四个数字可以组成没有重复数字且不能被5整除的四位数的个数是（ ）
| A、24个 | B、12个 |
| C、6个 | D、4个 |
已知定义在（0，π）的函数 f（x）=sinx-
x，则f（x）的单调递减区间为（ ）
| 1 |
| 2 |
| A、（0，π） | ||
B、（0，
| ||
C、（
| ||
D、（
|
已知在△ABC中，角A，B，C的对边分别为a，b，c，已知点D是边BC的中点，且2
•
=a2-ac，则B的大小为（ ）
| AD |
| BC |
| A、45° | B、60° |
| C、90° | D、120° |
已知p：∅⊆{0}；q：{1}∈{1，2}．由它们构成的以下三个命题中，真命题有（ ）
①p∧q ②p∨q ③￢p．
①p∧q ②p∨q ③￢p．
| A、1个 | B、2个 | C、3个 | D、0个 |
抛掷一枚骰子，得到偶数点的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|