题目内容
已知数列{an}满足:a1=
,an+1=
(n∈N*).
(1)求证:
≤an<1;
(2)设数列{an}的前n项和为Sn,求证:当n≥2时,|Sn-(
+
+…+
)|<
.
| 1 |
| 2 |
| 2an |
| 1+an2 |
(1)求证:
| 1 |
| 2 |
(2)设数列{an}的前n项和为Sn,求证:当n≥2时,|Sn-(
| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
| n-1 |
| 2 |
考点:数列与不等式的综合,数列递推式
专题:等差数列与等比数列
分析:(1)由完全平方差公式得an=
≤1,由a1=
,得an≠1,从而an<1,由
=
>1,得
≤an<1.
(2)由
≤an<1,得|Sn-(
+
+…+
)|<|(a1+a2+…+an)-(a1+
),由此能证明当n≥2时,|Sn-(
+
+…+
)|<
.
| 2an-1 |
| an-12+1 |
| 1 |
| 2 |
| an |
| an-1 |
| 2 |
| an-12+1 |
| 1 |
| 2 |
(2)由
| 1 |
| 2 |
| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
| ||||||||
| n-1个 |
| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
| n-1 |
| 2 |
解答:
(1)证明:∵an-12+1-2an-1=(an-1-1)2≥0,
a1=
,an+1=
(n∈N*),
∴an=
≤1
若an=1,则an-1=1,
∵a1=
,∴an≠1,∴an<1,
∵an-1<1,∴
=
>1,
∴{an}是增数列,∴
≤an<1.
(2)证明:∵
≤an<1,
∴当n≥2时,|Sn-(
+
+…+
)|
<|(a1+a2+…+an)-(a1+
)|
=|(a2+a3+…+an)-
|
<|
-
|=
.
∴当n≥2时,|Sn-(
+
+…+
)|<
.
a1=
| 1 |
| 2 |
| 2an |
| 1+an2 |
∴an=
| 2an-1 |
| an-12+1 |
若an=1,则an-1=1,
∵a1=
| 1 |
| 2 |
∵an-1<1,∴
| an |
| an-1 |
| 2 |
| an-12+1 |
∴{an}是增数列,∴
| 1 |
| 2 |
(2)证明:∵
| 1 |
| 2 |
∴当n≥2时,|Sn-(
| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
<|(a1+a2+…+an)-(a1+
| ||||||||
| n-1个 |
=|(a2+a3+…+an)-
| n-1 |
| 2 |
<|
| ||
| n-1个 |
| n-1 |
| 2 |
| n-1 |
| 2 |
∴当n≥2时,|Sn-(
| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
| n-1 |
| 2 |
点评:本题考查不等式的证明,是中档题,解题时要认真审题,注意数列的单调性和放缩法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
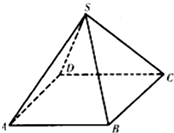 如图,四棱锥S-ABCD的底面是边长为2a的菱形,且SA=SC=2a,SB=SD=
如图,四棱锥S-ABCD的底面是边长为2a的菱形,且SA=SC=2a,SB=SD=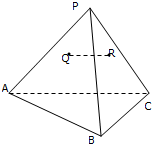 如图,已知P为△ABC所在平面内一点,Q、R是△PAB、△PBC的重心,求证:直线QR∥平面ABC.
如图,已知P为△ABC所在平面内一点,Q、R是△PAB、△PBC的重心,求证:直线QR∥平面ABC.