题目内容
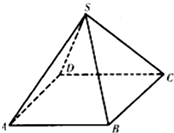 如图,四棱锥S-ABCD的底面是边长为2a的菱形,且SA=SC=2a,SB=SD=
如图,四棱锥S-ABCD的底面是边长为2a的菱形,且SA=SC=2a,SB=SD=| 2 |
(1)求证:对任意的λ∈(0,2],都有BD⊥AE;
(2)若SC⊥平面BED,求直线SA与平面BED所成角的大小.
考点:直线与平面所成的角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)连结BD,AC,设BD与AC交于O,由已知得BD⊥AC,BD⊥SO,由此能证明BD⊥面SAC,从而BD⊥AE.
(2)取SC的中点F,连结OF,OE,则SA∥OF,从而OF与平面EDB所成的角就是SA与平面EDB所成的角,进而∠EOF为所求角,由此能求出直线SA与平面BED所成角.
(2)取SC的中点F,连结OF,OE,则SA∥OF,从而OF与平面EDB所成的角就是SA与平面EDB所成的角,进而∠EOF为所求角,由此能求出直线SA与平面BED所成角.
解答:
(1)证明:连结BD,AC,设BD与AC交于O. (1分)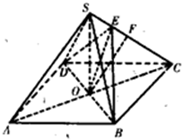
由底面是菱形,得BD⊥AC,(2分)
∵SB=SD,O为BD中点,∴BD⊥SO,(3分)
又AC∩SO=O,∴BD⊥面SAC,(4分)
又AE?面SAC,∴BD⊥AE.(5分)
(2)解:取SC的中点F,连结OF,OE,
∴SA∥OF,∴OF与平面EDB所成的角就是SA与平面EDB所成的角,(6分)
∵SC⊥平面BED,∴FE⊥面BED,E为垂足,∴∠EOF为所求角,(7分)
在等腰△CSB中,SC=BC=2a,SB=
a,得底边SB上的高为CH=
a,
∴SC•BE=SB•CH,∴BE=
=
a,(9分)
∴在Rt△BES中,SE=
=
a,
∴EF=a-
a=
a,(10分)
在Rt△FEO中,OF=a,∴sin∠EOF=
=
,(11分)
即直线SA与平面BED所成角为
.(12分)

由底面是菱形,得BD⊥AC,(2分)
∵SB=SD,O为BD中点,∴BD⊥SO,(3分)
又AC∩SO=O,∴BD⊥面SAC,(4分)
又AE?面SAC,∴BD⊥AE.(5分)
(2)解:取SC的中点F,连结OF,OE,
∴SA∥OF,∴OF与平面EDB所成的角就是SA与平面EDB所成的角,(6分)
∵SC⊥平面BED,∴FE⊥面BED,E为垂足,∴∠EOF为所求角,(7分)
在等腰△CSB中,SC=BC=2a,SB=
| 2 |
|
∴SC•BE=SB•CH,∴BE=
| ||||||
| 2a |
| ||
| 2 |
∴在Rt△BES中,SE=
2a2-
|
| 1 |
| 2 |
∴EF=a-
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△FEO中,OF=a,∴sin∠EOF=
| EF |
| OF |
| 1 |
| 2 |
即直线SA与平面BED所成角为
| π |
| 6 |
点评:本题考查异面直线垂直的证明,考查直线与平面所成角的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
“x,y∈R,x2+y2=0”是“xy=0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知集合M={x|y=
},N={x|y=log2(2-x)},则∁R(M∩N)( )
| x |
| A、[1,2) |
| B、(-∞,1)∪[2,+∞) |
| C、[0,1] |
| D、(-∞,0)∪[2,+∞) |
在极坐标系中,圆ρ=4sinθ的圆心到直线θ=
(θ∈R)的距离是( )
| π |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
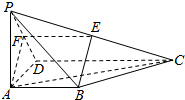 如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=PA=2,CD=4,E,F分别是PC,PD的中点.
如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=PA=2,CD=4,E,F分别是PC,PD的中点.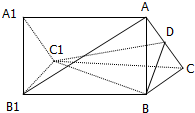 如图,已知A1B1C1-ABC是正三棱柱(底面为正三角形,且侧棱垂直底面),D是AC的中点.求证:AB1∥平面DBC1.
如图,已知A1B1C1-ABC是正三棱柱(底面为正三角形,且侧棱垂直底面),D是AC的中点.求证:AB1∥平面DBC1.