题目内容
若a1,a2∈R+,则有不等式
≥(
)2成立,请你类比推广此性质.
| (a1)2+(a2)2 |
| 2 |
| a1+a2 |
| 2 |
考点:类比推理
专题:计算题,推理和证明
分析:掌握好类比推理的方法,由此得出结论即可.
解答:
解:∵a1,a2∈R+,则有不等式
≥(
)2成立,
∴类比推广可得(a12+a22+…+an2)(12+12+…+12)≥(a1+a2+…+an)2.
| (a1)2+(a2)2 |
| 2 |
| a1+a2 |
| 2 |
∴类比推广可得(a12+a22+…+an2)(12+12+…+12)≥(a1+a2+…+an)2.
点评:本题主要考查了类比推理的方法的运用,属于中档题,解答此题的关键是掌握好类比推理的方法.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知a=(
)0.5,b=2-0.3,c=log23,则a,b,c大小关系为( )
| 1 |
| 2 |
| A、b>a>c |
| B、a>c>b |
| C、c>b>a |
| D、a>b>c |
若向量
=(-1,0,1),向量
=(2,0,k),且满足向量
∥
,则k等于( )
| a |
| b |
| a |
| b |
| A、1 | B、-1 | C、2 | D、-2 |
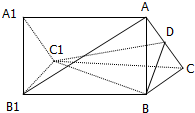 如图,已知A1B1C1-ABC是正三棱柱(底面为正三角形,且侧棱垂直底面),D是AC的中点.求证:AB1∥平面DBC1.
如图,已知A1B1C1-ABC是正三棱柱(底面为正三角形,且侧棱垂直底面),D是AC的中点.求证:AB1∥平面DBC1.