题目内容
若不等式
≤k的解集是空集,则正整数k的取值集合为 .
| 3x2+2x+2 |
| x2+x+1 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:根据不等式的解集是空集,转化为一元二次不等式,进行求解即可.
解答:
解:不等式
≤k的解集是空集,
等价为3x2+2x+2≤k(x2+x+1),
即(3-k)x2+(2-k)x+2-k≤0的解集是空集,
若k=3,不等式等价为x≥1,此时不满足条件.
若3-k<0,即k>3,不等式(3-k)x2+(2-k)x+2-k≤0的解集不是空集,不满足条件,
若3-k>0,即k<3,若(3-k)x2+(2-k)x+2-k≤0的解集是空集,
则等价为判别式△=(2-k)2-4(3-k)(2-k)=(2-k)(3k-10)<0,
解得k>
或k<2,
∵k<3,
∴k<2,
∵k是正整数,
∴k=1,
故答案为:{1}
| 3x2+2x+2 |
| x2+x+1 |
等价为3x2+2x+2≤k(x2+x+1),
即(3-k)x2+(2-k)x+2-k≤0的解集是空集,
若k=3,不等式等价为x≥1,此时不满足条件.
若3-k<0,即k>3,不等式(3-k)x2+(2-k)x+2-k≤0的解集不是空集,不满足条件,
若3-k>0,即k<3,若(3-k)x2+(2-k)x+2-k≤0的解集是空集,
则等价为判别式△=(2-k)2-4(3-k)(2-k)=(2-k)(3k-10)<0,
解得k>
| 10 |
| 3 |
∵k<3,
∴k<2,
∵k是正整数,
∴k=1,
故答案为:{1}
点评:本题主要考查不等式的求解,根据不等式的解集,转化为不等式恒成立是解决本题的关键.

练习册系列答案
相关题目
已知底面是边长为1的正方形,侧棱长为
且侧棱与底面垂直的四棱柱的各顶点均在同一个球面上,则该球的体积为( )
| 2 |
A、
| ||
| B、4π | ||
| C、2π | ||
D、
|
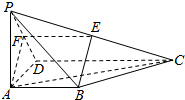 如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=PA=2,CD=4,E,F分别是PC,PD的中点.
如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=PA=2,CD=4,E,F分别是PC,PD的中点.