题目内容
(1)从若干张扑克牌中随机抽取一张,如果取到红心(事件A)的概率是
,取到方片(事件B)的概率是
.求:取到红色牌(事件C)的概率,取到黑色牌(事件D)的概率;
(2)同时掷两个骰子,计算向上的点数之和是6的概率.
| 1 |
| 4 |
| 1 |
| 4 |
(2)同时掷两个骰子,计算向上的点数之和是6的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:计算题,概率与统计
分析:(1)利用概率的基本性质解答;(2)其概率模型为古典概型.
解答:
解:(1)由题意,事件C是事件A与B的和,且事件A与B互斥,
则P(C)=
+
=
;
∵事件C与事件D是对立事件,
则P(D)=1-P(c)=
.
(2)其概率模型为古典概型,
符合题意的有(1,5),(2,4),(3,3),(4,2),(5,1)共5个.
则其概率P=
=
;
故答案为:
.
则P(C)=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∵事件C与事件D是对立事件,
则P(D)=1-P(c)=
| 1 |
| 2 |
(2)其概率模型为古典概型,
符合题意的有(1,5),(2,4),(3,3),(4,2),(5,1)共5个.
则其概率P=
| 5 |
| 6×6 |
| 5 |
| 36 |
故答案为:
| 5 |
| 36 |
点评:本题考查了古典概型概率的求法及概率的基本性质,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
下列说法正确的是( )
| A、三点确定一个平面 |
| B、四边形一定是平面图形 |
| C、梯形一定是平面图形 |
| D、平面α和平面β有不同在一条直线上的三个公共点 |
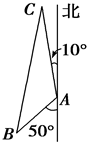 我舰在岛A南偏西50°相距12海里的B处发现敌舰正从岛A沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求我舰航行速度.
我舰在岛A南偏西50°相距12海里的B处发现敌舰正从岛A沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求我舰航行速度.