题目内容
已知二次函数f(x)的二次项系数为a,且不等式f(x)>-4x的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的实根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求a的取值范围.
(1)若方程f(x)+6a=0有两个相等的实根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)设f(x)=ax2+bx+c,(a<0),由题意得方程f(x)=-4x两个根是1,3,由韦达定理求得b=-4a-4,c=3a,可得f(x)=ax2-4(a+1)x+3a.再根据△=16(a+1)2-36a2=0,解得a的值,可得f(x)的解析式.
(2)由题意可得
>0,再由a<0可得 a2+8a+4>0,由此求得a的范围.
(2)由题意可得
| 12a2-16(a+1)2 |
| 4a |
解答:
解:(1)设f(x)=ax2+bx+c,(a<0),由题意得方程f(x)=-4x两个根是1,3,
即ax2+(b+4)x+c=0两个根是1,3,故由韦达定理可得-
=4,
=3,∴b=-4a-4,c=3a,f(x)=ax2-4(a+1)x+3a.
再根据方程f(x)+6a=0,即ax2-4(a+1)x+9a=0有两个相等的实根,∴△=16(a+1)2-36a2=0,解得a=-
,
∴f(x)=-
x2-
x-
.
(2)由于f(x)=ax2-4(a+1)x+3a 的最大值为正数,可得
>0,即
<0,
再由a<0可得 a2+8a+4>0,求得 a<-4-2
,或-4+2
<a<0,
即a的范围是:{a|a<-4-2
,或-4+2
<a<0 }.
即ax2+(b+4)x+c=0两个根是1,3,故由韦达定理可得-
| b+4 |
| a |
| c |
| a |
再根据方程f(x)+6a=0,即ax2-4(a+1)x+9a=0有两个相等的实根,∴△=16(a+1)2-36a2=0,解得a=-
| 2 |
| 5 |
∴f(x)=-
| 2 |
| 5 |
| 12 |
| 5 |
| 6 |
| 5 |
(2)由于f(x)=ax2-4(a+1)x+3a 的最大值为正数,可得
| 12a2-16(a+1)2 |
| 4a |
| a2+8a+4 |
| a |
再由a<0可得 a2+8a+4>0,求得 a<-4-2
| 3 |
| 3 |
即a的范围是:{a|a<-4-2
| 3 |
| 3 |
点评:本题主要考查二次函数的性质,用待定系数法求函数的解析式,分式不等式的解法,体现了转化的数学思想,属于基础题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
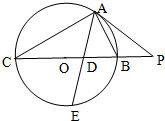 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.