题目内容
设函数f(x)=
(a∈R).若方程f(f(x))=x有解,则a的取值范围为( )
| x-a |
A、(-∞,
| ||
B、(0,
| ||
C、(-∞,
| ||
| D、[1,+∞) |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:设f(x)=t,则方程等价为f(t)=x,根据条件将方程转化为含有x的一元二次函数,利用二次函数的图象和性质进行求解即可.
解答:
解:设f(x)=t,t≥0,则方程f(f(x))=x等价为f(t)=x,
即
,
∴t=x,
即f(x)=x,
∴
=x在x≥0时有解,
即x-a=x2,
∴a=-x2+x在x≥0时成立,
设g(x)=-x2+x=-(x2-x)=-(x-
)2+
,
∵x≥0
∴当x=
时,g(x)取得最大值
,
∴g(x)≤
,
即a≤
,
故选:A.
即
|
∴t=x,
即f(x)=x,
∴
| x-a |
即x-a=x2,
∴a=-x2+x在x≥0时成立,
设g(x)=-x2+x=-(x2-x)=-(x-
| 1 |
| 2 |
| 1 |
| 4 |
∵x≥0
∴当x=
| 1 |
| 2 |
| 1 |
| 4 |
∴g(x)≤
| 1 |
| 4 |
即a≤
| 1 |
| 4 |
故选:A.
点评:本题主要考查方程有解的判断,利用换元法将方程进行转化,利用二次函数的图象和性质是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目
直线y=x-1被椭圆x2+4y2=4截得的弦长为( )
A、
| ||||
B、
| ||||
C、3或
| ||||
D、
|
已知函数f(x)=
,若|f(x)|≥ax-2,则a的取值范围是( )
|
| A、[-2,2] | ||
| B、[-2,0] | ||
C、[1-2
| ||
D、[1-2
|
直线x-y+3=0的倾斜角是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知正数a,b满足:三数a,1,b的倒数成等差数列,则a+b的最小值为( )
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
已知x0是函数f(x)=(
)x-
的一个零点,若x1∈(0,x0),x2∈(x0,+∞),则( )
| 1 |
| 2 |
| x |
| A、f(x1)<0,f(x2)<0 |
| B、f(x1)>0,f(x2)<0 |
| C、f(x1)<0,f(x2)>0 |
| D、f(x1)>0,f(x2)>0 |
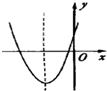 二次函数y=ax2+bx+c的图象如图所示,则a+b+c
二次函数y=ax2+bx+c的图象如图所示,则a+b+c