题目内容
已知函数f(x)是定义在R上的偶函数,且x≥0时,f(x)=(
)x,函数f(x)的值域为集合A.
(1)求f(-1)的值;
(2)求f(x)的解析式;
(3)设函数g(x)=
的定义域为集合B,若A⊆B,求实数a的取值范围.
| 1 |
| 2 |
(1)求f(-1)的值;
(2)求f(x)的解析式;
(3)设函数g(x)=
| -x2+(a-1)x+a |
考点:指数函数综合题
专题:函数的性质及应用
分析:(1)由偶函数的定义可得f(-1)=f(1),再根据x≥0时,f(x)=(
)x,求得结果.
(2)设x<0,则-x>0,再根据x≥0时,f(x)=(
)x,以及函数为偶函数求得f(x)的解析式,从而求得f(x)在R上的解析式.
(3)由(2)求得A=(0,1].再由函数g(x)的解析式可得-(x-a)(x+1)≥0.分类讨论结合A⊆B,可得a的范围.
| 1 |
| 2 |
(2)设x<0,则-x>0,再根据x≥0时,f(x)=(
| 1 |
| 2 |
(3)由(2)求得A=(0,1].再由函数g(x)的解析式可得-(x-a)(x+1)≥0.分类讨论结合A⊆B,可得a的范围.
解答:
解:(1)由偶函数的定义可得f(-1)=f(1)=(
)1=
.
(2)设x<0,则-x>0,再根据x≥0时,f(x)=(
)x,
可得 f(-x)=(
)-x=2x.
综上可得,f(x)=
.
(3)由(2)可得函数f(x)的值域A=(0,1].
函数g(x)=
=
,可得-(x-a)(x+1)≥0.
当a<-1时,g(x)的定义域为B=(a,-1),再由A⊆B,可得a∈∅.
当a>-1时,g(x)的定义域为B=(-1,a),再由A⊆B,可得a>1.
当a=-1时,B={-1},不满足A⊆B.
综上可得,a的范围为(1,+∞).
| 1 |
| 2 |
| 1 |
| 2 |
(2)设x<0,则-x>0,再根据x≥0时,f(x)=(
| 1 |
| 2 |
可得 f(-x)=(
| 1 |
| 2 |
综上可得,f(x)=
|
(3)由(2)可得函数f(x)的值域A=(0,1].
函数g(x)=
| -x2+(a-1)x+a |
| -(x-a)(x+1) |
当a<-1时,g(x)的定义域为B=(a,-1),再由A⊆B,可得a∈∅.
当a>-1时,g(x)的定义域为B=(-1,a),再由A⊆B,可得a>1.
当a=-1时,B={-1},不满足A⊆B.
综上可得,a的范围为(1,+∞).
点评:本题主要考查函数的奇偶性的应用,求函数的解析式,二次函数的性质应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
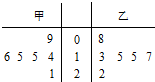 甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,x1,x2分别表示甲乙两名运动员这项测试成绩的众数,s1,s2分别表示甲乙两名运动员这项测试成绩的标准差,则有( )
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,x1,x2分别表示甲乙两名运动员这项测试成绩的众数,s1,s2分别表示甲乙两名运动员这项测试成绩的标准差,则有( )| A、x1>x2,s1<s2 |
| B、x1=x2,s1<s2 |
| C、x1=x2,s1=s2 |
| D、x1=x2,s1>s2 |
若f(x)=
,则f(2016)等于( )
|
| A、0 |
| B、ln2 |
| C、1+e2 |
| D、1+ln2 |
设函数f(x)=
(a∈R).若方程f(f(x))=x有解,则a的取值范围为( )
| x-a |
A、(-∞,
| ||
B、(0,
| ||
C、(-∞,
| ||
| D、[1,+∞) |
数列{an}中a1=1,a5=13,an+2+an=2an+1;数列{bn}中,b2=6,b3=3,bn+2bn=b
,在直角坐标平面内,已知点列P1(a1,b1),P2(a2,b2),P3(a3,b3),…,Pn(an,bn)…,则向量
+
+
+…+
的坐标为( )
2 n+1 |
| P1P2 |
| P3P4 |
| P5P6 |
| P2009P2010 |
A、(3015,8[(
| ||
B、(3012,8[(
| ||
C、(3015,8[(
| ||
D、(3018,8[(
|