题目内容
已知正数a,b满足:三数a,1,b的倒数成等差数列,则a+b的最小值为( )
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
考点:等差数列的性质
专题:等差数列与等比数列
分析:由三数a,1,b的倒数成等差数列,列式得到
+
=2,把a+b化为
(a+b)(
+
)展开后利用基本不等式求最值.
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| b |
解答:
解:∵三数a,1,b的倒数成等差数列,
∴
+
=2,
则a+b=
(a+b)(
+
)=
[1+
+
+1]≥
(2+2
)=2.
∴a+b的最小值为2.
故选:B.
∴
| 1 |
| a |
| 1 |
| b |
则a+b=
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| a |
| b |
| b |
| a |
| 1 |
| 2 |
|
∴a+b的最小值为2.
故选:B.
点评:本题考查了等差数列的性质,考查了利用基本不等式求最值,是基础的计算题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
设函数f(x)=
(a∈R).若方程f(f(x))=x有解,则a的取值范围为( )
| x-a |
A、(-∞,
| ||
B、(0,
| ||
C、(-∞,
| ||
| D、[1,+∞) |
数列{an}中a1=1,a5=13,an+2+an=2an+1;数列{bn}中,b2=6,b3=3,bn+2bn=b
,在直角坐标平面内,已知点列P1(a1,b1),P2(a2,b2),P3(a3,b3),…,Pn(an,bn)…,则向量
+
+
+…+
的坐标为( )
2 n+1 |
| P1P2 |
| P3P4 |
| P5P6 |
| P2009P2010 |
A、(3015,8[(
| ||
B、(3012,8[(
| ||
C、(3015,8[(
| ||
D、(3018,8[(
|
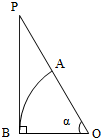 如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
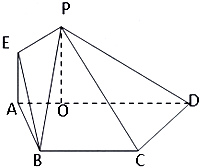 如图,在等腰梯形ABCD中,AD∥BC,
如图,在等腰梯形ABCD中,AD∥BC,