题目内容
已知函数f（x）=3sin（ωx+
）（ω＞0）和g（x）=2cos（2x+φ）+1（|φ|＜
）的图象的对称轴完全相同，则φ= ．
| π |
| 6 |
| π |
| 2 |
考点：正弦函数的对称性
专题：三角函数的图像与性质
分析：由题意可得，函数f（x）和g（x）的周期相同，故有ω=2，f（x）=3sin（2x+
）．再根据当2x+
=2kπ+
，k∈z，函数f（x）和g（x）同时取到取得最大值，求得φ的值．
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解答：
解：由题意可得，函数f（x）和g（x）的周期相同，故有ω=2，f（x）=3sin（2x+
）．
再根据当2x+
=2kπ+
，k∈z，即x=kπ+
时，函数f（x）取得最大值，
可得g（x）=2cos[2•（kπ+
）+φ]+1=2cos（2kπ+
+φ）+1也取得最大值，故2kπ+
+φ=2nπ，n∈z．
再结合|φ|＜
可得 φ=-
，
故答案为：-
．
| π |
| 6 |
再根据当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
可得g（x）=2cos[2•（kπ+
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
再结合|φ|＜
| π |
| 2 |
| π |
| 3 |
故答案为：-
| π |
| 3 |
点评：本题主要考查正弦函数和余弦函数的图象的对称性，属于基础题．
练习册系列答案
相关题目
已知△ABC是边长为2的正三角形，则它的平面直观图△A′B′C′的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中，值域为（0，+∞）的是（ ）
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
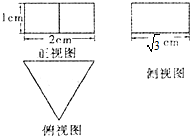某个几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的表面积是（ ）A、
| ||
B、6+
| ||
C、6+2
| ||
D、6+3
|
