题目内容
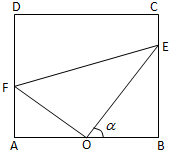 合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50
合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50| 3 |
(1)设∠BOE=α,试将△OEF的周长L表示成α的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为800元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
考点:根据实际问题选择函数类型
专题:应用题,函数的性质及应用
分析:(1)在直角三角形中写出三边长的公式,从而得到周长公式,根据题意写出定义域即可;
(2)利用换元法,设t=sinα+cosα,α∈[
,
],从而得到l=
=
∈[100(
+1),100(
+1)],从而求最小值.
(2)利用换元法,设t=sinα+cosα,α∈[
| π |
| 6 |
| π |
| 3 |
| 50(t+1) | ||
|
| 100 |
| t-1 |
| 2 |
| 3 |
解答:
解:(1)在Rt△BOE中,OE=
,
在Rt△AOF中,OF=
在Rt△OEF中,EF=
,
当点F在点D时,角α最小,α=
,
当点E在点C时,角α最大,α=
,
则l=
,
定义域为[
,
].
(2)设t=sinα+cosα,α∈[
,
],
则
≤t≤
,
l=
=
∈[100(
+1),100(
+1)].
则当α=
时,lmin=100(
+1),
总费用最低为80000(
+1)元.
| 50 |
| cosα |
在Rt△AOF中,OF=
| 50 |
| sinα |
在Rt△OEF中,EF=
| 50 |
| sinαcosα |
当点F在点D时,角α最小,α=
| π |
| 6 |
当点E在点C时,角α最大,α=
| π |
| 3 |
则l=
| 50(sinα+cosα+1) |
| sinαcosα |
定义域为[
| π |
| 6 |
| π |
| 3 |
(2)设t=sinα+cosα,α∈[
| π |
| 6 |
| π |
| 3 |
则
| ||
| 2 |
| 2 |
l=
| 50(t+1) | ||
|
| 100 |
| t-1 |
| 2 |
| 3 |
则当α=
| π |
| 4 |
| 2 |
总费用最低为80000(
| 2 |
点评:本题考查了学生将实际问题转化为数学问题的能力及最值的求法,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
已知函数f(x)=alog2x+blog4x+2,且f(
)=4,则f(2014)的值为( )
| 1 |
| 2014 |
| A、-4 | B、2 | C、0 | D、-2 |
已知曲线C:f(x)=x3-ax+a,若过曲线C外一点A(1,0)引曲线C的两条切线,它们的倾斜角互补,则a的值为( )
A、
| ||
| B、-2 | ||
| C、2 | ||
D、-
|
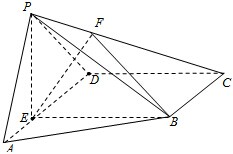 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.