题目内容
定义运算:a*b=
,则函数f(x)=x*
的值域为 .
|
| 1 |
| x-1 |
考点:函数的值域
专题:函数的性质及应用
分析:由新定义确定分段函数在各段上f(x)的表达式,画函数的图象,从而求出值域.
解答:
解:由题意,
①当x×
>0时,也即x<0\或x>1时,函数f(x)=x;
①当x×
≤0时,也即0≤x<1时,函数f(x)=
;
函数f(x)的图象:

从图象上得知:函数f(x)的值域是(-∞,0)∪(1,+∞).
故答案为:(-∞,0)∪(1,+∞).
①当x×
| 1 |
| x-1 |
①当x×
| 1 |
| x-1 |
| 1 |
| x-1 |
函数f(x)的图象:

从图象上得知:函数f(x)的值域是(-∞,0)∪(1,+∞).
故答案为:(-∞,0)∪(1,+∞).
点评:考查了函数的值域的求法,同时考查了学生对新定义的接受能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果曲线C上任意一点的坐标都是方程F(x,y)=0的解,那么下列命题正确的是( )
| A、曲线C的方程是F(x,y)=0 |
| B、曲线C上的点都在方程F(x,y)=0的曲线上 |
| C、方程F(x,y)=0的曲线是C |
| D、以方程F(x,y)=0解为坐标点都在曲线C上 |
已知函数f(x)=alog2x+blog4x+2,且f(
)=4,则f(2014)的值为( )
| 1 |
| 2014 |
| A、-4 | B、2 | C、0 | D、-2 |
命题甲:若x,y∈R,则|x|>1是x>1是充分而不必要条件;命题乙:函数y=
的定义域是(-∞,-1]∪[3,+∞),则( )
| |x-1|-2 |
| A、“甲或乙”为假 |
| B、“甲且乙”为真 |
| C、甲真乙假 |
| D、甲假乙真 |
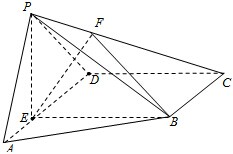 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.