题目内容
已知函数f(x)=x-
的图象的经过点(2,1)
(1)求a的值;
(2)判断f(x)的奇偶性.
| a |
| x |
(1)求a的值;
(2)判断f(x)的奇偶性.
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:(1)根据条件,即可求a的值;
(2)根据函数的奇偶性的定义即可判断f(x)的奇偶性.
(2)根据函数的奇偶性的定义即可判断f(x)的奇偶性.
解答:
解:(1)由题意可得f(2)=1-
=1,所以a=2.
(2)由(1)得f(x)=x-
=x-
,则f(z)的定义域为(0,+∞)∪(0,+∞).
所以f(-x)=-x-
=-x+
=-f(x).
故f(x)为奇函数.
| a |
| 2 |
(2)由(1)得f(x)=x-
| a |
| x |
| 2 |
| x |
所以f(-x)=-x-
| 2 |
| -x |
| 2 |
| x |
故f(x)为奇函数.
点评:本题主要考查函数奇函数的求解,根据函数奇偶性的定义是解决本题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
不等式x2-2x+5≥a2-3a对任意实数x恒成立,则实数a的取值范围为( )
| A、[-1,4] |
| B、(-∞,-2]∪[5,+∞) |
| C、(-∞,-1]∪[4,+∞) |
| D、[-2,5] |
已知数列{an}是等比数列,Sn是其前n项和,且a3=2,S3=6,则a5=( )
A、2或-
| ||
B、
| ||
| C、±2 | ||
D、2或
|
若m>0,n>0,a>0且a≠1,则下列等式中正确的是( )
| A、(am)n=am+n | |||||
B、a
| |||||
| C、logam÷logan=loga(m-n) | |||||
D、
|
二次函数f(x)=x2-4x(x∈[0,5))的值域为( )
| A、[-4,+∞) |
| B、[-4,5] |
| C、[-4,5) |
| D、[0,5) |
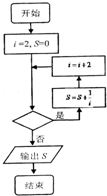
如图给出的是计算
+
+
+…+
的值的程序框图,其中判断框内应填入的是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2014 |

| A、i≤2013 |
| B、i≤2015 |
| C、i≤2017 |
| D、i≤2019 |
已知复数z1=2+ai(a∈R),z2=1-2i,若
为纯虚数,则|z1|=( )
| z1 |
| z2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|