Question

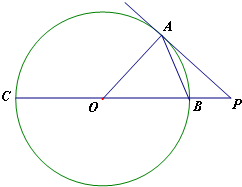如图，点A在直径为15的⊙O上，PBC是过点O的割线，且PA=10，PB=5．
（Ⅰ）求证：PA与⊙O相切；
（Ⅱ）求S△_ACB的值．

Answer 1

考点：圆的切线的判定定理的证明

专题：选作题,立体几何

分析：（Ⅰ）利用勾股定理证明PA⊥OA，再利用切线的判定方法，即可得出结论；
（Ⅱ）证明△PAB∽△PCA，可得

AB

AC

=

PB

PA

=

5

10

=

1

2

，求出AC，BC，即可求S△_ACB的值．

解答： （Ⅰ）证明：连结OA，
∵⊙O的直径为15，∴OA=OB=7.5
又PA=10，PB=5，∴PO=12.5…（2分）
在△APO中，PO²=156.25，PA²+OA²=156.25
即PO²=PA²+OA²，∴PA⊥OA，
又点A在⊙O上
故PA与⊙O相切…（5分）
（Ⅱ）解：∵PA为⊙O的切线，∴∠ACB=∠PAB，
又由∠P=∠P，∴△PAB∽△PCA，∴

AB

AC

=

PB

PA

=

5

10

=

1

2

…（7分）
设AB=k，AC=2k，∵BC为⊙O的直径且BC=15，AB⊥AC
∴BC=

k2+(2k)2

=

5

k=15，
∴k=3

5

∴S△ACB=

1

2

AC•AB=

1

2

•2k•k=k2=45…（10分）

点评：本题考查了切线的判定与性质．解答这类题目，常见的辅助线有：
①判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”；
②有切线时，常常“遇到切点连圆心得半径”．