题目内容
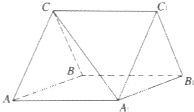 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.(Ⅰ)若点M、N分别是边A1B1、BC的中点,求证:MN∥平面ACC1A1
(Ⅱ)证明:AB⊥A1C;
(Ⅲ)若AB=CB=2,A1C=
| 6 |
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间角
分析:(Ⅰ)取AC中点D,连结DA1,DN,由已知条件推导出四边形A1MND为平行四边形,由此能证明MN∥平面ACC1A1.
(Ⅱ)取AB中点E,连结EC,EA,由已知条件推导出EC⊥AB,A1E⊥AB,由此能证明AB⊥平面A1EC,从而得到AB⊥A1C.
(Ⅲ)以E为原点,EA为x轴,以EA1为y轴,以EC为z轴,建立空间直角坐标系,利用向量法能求出二面角B-AC-A1的余弦值.
(Ⅱ)取AB中点E,连结EC,EA,由已知条件推导出EC⊥AB,A1E⊥AB,由此能证明AB⊥平面A1EC,从而得到AB⊥A1C.
(Ⅲ)以E为原点,EA为x轴,以EA1为y轴,以EC为z轴,建立空间直角坐标系,利用向量法能求出二面角B-AC-A1的余弦值.
解答:
(Ⅰ)证明:如图,取AC中点D,连结DA1,DN,
∵N为BC有中点,∴在△ABC中,ND
AB,
又∵M为A1B1中点,A1B1∥AB,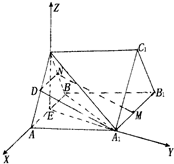
∴A1M
AB,∴ND
A1M,
∴四边形A1MND为平行四边形,∴MN∥A1D,
又∵MN不包含于平面ACC1A1,AD1?平面ACC1A1,
∴MN∥平面ACC1A1.
(Ⅱ)证明:取AB中点E,连结EC,EA,
在△ABC中,CA=CB,∴EC⊥AB,
又在△AA1B中,AB=AA1,∠BAA1=60°,
∴△AA1B为正三角形,∴A1E⊥AB,
又A1E∩EC=E,
∴AB⊥平面A1EC,
∵A1C?平面A1EC,∴AB⊥A1C.
(Ⅲ)解:∵CA=CB,AB=CB=2,
∴△ABC为边长为2的正三角形,且CE=
,∴A1E=
,
又A1C=
,∴A1E2+CE2=6=A1C2,
∴EC⊥EA1,又EC⊥AB,EA1∩AB=E,
∴以E为原点,EA为x轴,以EA1为y轴,以EC为z轴,建立空间直角坐标系,
∴A(1,0,0),A1(0,
,0),C(0,0,
),
∴
=(-1,0,
),
=(-1,
,0),
=(0,
,0),
∵EA1⊥平面ABC,∴
=(0,
,0)是平面ABC的法向量,
设平面AA1C的法向量为
=(x,y,z),
则有
,
取x=
,得
=(
,1,1),
∴cos<
,
>=
=
,
∴二面角B-AC-A1的余弦值为
.
∵N为BC有中点,∴在△ABC中,ND
| ∥ |
. |
| 1 |
| 2 |
又∵M为A1B1中点,A1B1∥AB,

∴A1M
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∴四边形A1MND为平行四边形,∴MN∥A1D,
又∵MN不包含于平面ACC1A1,AD1?平面ACC1A1,
∴MN∥平面ACC1A1.
(Ⅱ)证明:取AB中点E,连结EC,EA,
在△ABC中,CA=CB,∴EC⊥AB,
又在△AA1B中,AB=AA1,∠BAA1=60°,
∴△AA1B为正三角形,∴A1E⊥AB,
又A1E∩EC=E,
∴AB⊥平面A1EC,
∵A1C?平面A1EC,∴AB⊥A1C.
(Ⅲ)解:∵CA=CB,AB=CB=2,
∴△ABC为边长为2的正三角形,且CE=
| 3 |
| 3 |
又A1C=
| 6 |
∴EC⊥EA1,又EC⊥AB,EA1∩AB=E,
∴以E为原点,EA为x轴,以EA1为y轴,以EC为z轴,建立空间直角坐标系,
∴A(1,0,0),A1(0,
| 3 |
| 3 |
∴
| AC |
| 3 |
| AA1 |
| 3 |
| EA1 |
| 3 |
∵EA1⊥平面ABC,∴
| EA1 |
| 3 |
设平面AA1C的法向量为
| n |
则有
|
取x=
| 3 |
| n |
| 3 |
∴cos<
| n |
| EA1 |
| ||||
|
| ||
| 5 |
∴二面角B-AC-A1的余弦值为
| ||
| 5 |
点评:本题考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
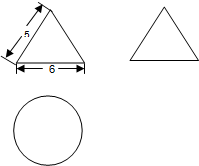 一个几何体的三视图及其尺寸如下(单位cm),则该几何体的表面积及体积为(cm2\cm3)( )
一个几何体的三视图及其尺寸如下(单位cm),则该几何体的表面积及体积为(cm2\cm3)( )| A、24π,12π |
| B、15π,12π |
| C、24π,36π |
| D、以上都不正确 |
函数y=
的定义域为( )
| sinx |
| A、[0,π] |
| B、x为第Ⅰ、Ⅱ象限的角 |
| C、{x|2kπ≤x≤(2k+1)π,k∈z} |
| D、(0,π) |
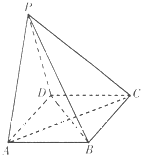 如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=
如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=