题目内容
已知A,B,C是圆O:x2+y2=1上任意的不同三点,若
=3
+x
,则正实数x的取值范围为( )
| OA |
| OB |
| OC |
| A、(0,2) |
| B、(1,4) |
| C、(2,4) |
| D、(3,4) |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:三点A,B,C在圆O:x2+y2=1上,所以|OA|=|OB|=|OC|=1,所以可以想到对
=3
+x
两边进行平方,从而去掉向量符号,得到1=9+6xcos<
,
>+x2,并求出cos<
,
>=
.可以判断<
,
>∈(0,π),所以-1<
<1,解该不等式即得x的取值范围.
| OA |
| OB |
| OC |
| OB |
| OC |
| OB |
| OC |
| -x2-8 |
| 6x |
| OB |
| OC |
| -x2-8 |
| 6x |
解答:
解:根据已知条件知:|
|=|
|=|
|=1;
∴对
=3
+x
两边平方可得:1=9+6xcos<
,
>+x2;
∵x>0,∴cos<
,
>=
;
∵A,B,C是不同三点;
∴-1<cos<
,
><1,∴-1<
<1;
∴
,解得2<x<4;
∴正实数x的取值范围为(2,4).
故选C.
| OA |
| OB |
| OC |
∴对
| OA |
| OB |
| OC |
| OB |
| OC |
∵x>0,∴cos<
| OB |
| OC |
| -x2-8 |
| 6x |
∵A,B,C是不同三点;
∴-1<cos<
| OB |
| OC |
| -x2-8x |
| 6x |
∴
|
∴正实数x的取值范围为(2,4).
故选C.
点评:考查向量的长度的概念,向量数量积的计算公式,向量夹角的概念及范围,以及解分式不等式,一元二次不等式组.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
点A、B、C、D在同一个球的球面上,且AB=CD=
,BC=2AC=2BD=2,则该球的表面积为( )
| 3 |
| A、16π | B、12π |
| C、8π | D、4π |
 已知函数f(x)=x-
已知函数f(x)=x-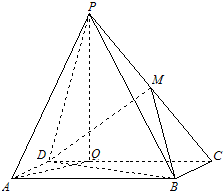 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,点P在底面的射影Q在CD上,且PQ=
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,点P在底面的射影Q在CD上,且PQ=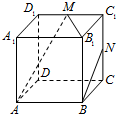 如图所示,在正方体ABCD A1B1C1D1中,M、N分别是棱C1D1,C1C的中点.给出以下四个结论:
如图所示,在正方体ABCD A1B1C1D1中,M、N分别是棱C1D1,C1C的中点.给出以下四个结论: