题目内容
给出下列四个命题:
①如果平面α与平面β相交,那么平面α内所有的直线都与平面β相交;
②如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β;
③如果平面α⊥平面β,那么平面α内与它们的交线不垂直的直线与平面β也不垂直;
④如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β.
真命题的序号是 .(写出所有真命题的序号)
①如果平面α与平面β相交,那么平面α内所有的直线都与平面β相交;
②如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β;
③如果平面α⊥平面β,那么平面α内与它们的交线不垂直的直线与平面β也不垂直;
④如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β.
真命题的序号是
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①根据两个平面相交的性质判断即可
②根据两个平面垂直相交的性质判断即可
③与④都用反证法证明即可
②根据两个平面垂直相交的性质判断即可
③与④都用反证法证明即可
解答:
解:如上图
对于①结论是不正确的,设α∩β=l,那么平面α内所有与l平行的直线都与平面β不相交;
对于②结论是不正确的,设α∩β=l,那么平面α内所有与l平行的直线都与平面β不垂直.
对于③结论是正确的,如上图,设α⊥β,α∩β=l,m?α,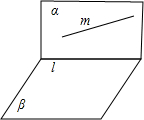
若直线m与l不垂直,则直线m与平面β不垂直.否则,m⊥β,则m⊥l,这与已知矛盾.
对于④结论是正确的.用反证法,假如平面α内一定存在直线m垂直于平面β,那么α⊥β,这与已知矛盾.
综上,①②是不正确的,③④是正确的.
故答案为:③④

对于①结论是不正确的,设α∩β=l,那么平面α内所有与l平行的直线都与平面β不相交;
对于②结论是不正确的,设α∩β=l,那么平面α内所有与l平行的直线都与平面β不垂直.
对于③结论是正确的,如上图,设α⊥β,α∩β=l,m?α,

若直线m与l不垂直,则直线m与平面β不垂直.否则,m⊥β,则m⊥l,这与已知矛盾.
对于④结论是正确的.用反证法,假如平面α内一定存在直线m垂直于平面β,那么α⊥β,这与已知矛盾.
综上,①②是不正确的,③④是正确的.
故答案为:③④
点评:本题考查了空间直线与平面的位置关系,属于基础题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知A,B,C是圆O:x2+y2=1上任意的不同三点,若
=3
+x
,则正实数x的取值范围为( )
| OA |
| OB |
| OC |
| A、(0,2) |
| B、(1,4) |
| C、(2,4) |
| D、(3,4) |