题目内容
已知函数f(x)=
(其中k∈R),f′(x)为f(x)的导函数.
(Ⅰ)求证:曲线y=f(x)在点(1,f(1))处的切线不过点(2,0);
(Ⅱ)若在区间(0,1]中存在x0,使得f′(x0)=0,求k的取值范围;
(Ⅲ)若f′(1)=0,试证明:对任意x>0,f′(x)<
恒成立.
| lnx+k |
| ex |
(Ⅰ)求证:曲线y=f(x)在点(1,f(1))处的切线不过点(2,0);
(Ⅱ)若在区间(0,1]中存在x0,使得f′(x0)=0,求k的取值范围;
(Ⅲ)若f′(1)=0,试证明:对任意x>0,f′(x)<
| e-2+1 |
| x2+x |
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(Ⅰ)求出曲线y=f(x)在点(1,f(1))处的切线方程,代入点(2,0)验证,即可得出结论;
(Ⅱ)由f′(x0)=0得k=
,确定其单调性,可求k的取值范围;
(Ⅲ)令g(x)=(x2+x)f′(x),对任意x>0,g(x)<e-2+1等价于1-x-xlnx<
(e-2+1).再构造函数,研究单调性,即可证明结论.
(Ⅱ)由f′(x0)=0得k=
| 1-x0lnx0 |
| x0 |
(Ⅲ)令g(x)=(x2+x)f′(x),对任意x>0,g(x)<e-2+1等价于1-x-xlnx<
| ex |
| x+1 |
解答:
(Ⅰ)证明:由f(x)=
得f′(x)=
,x∈(0,+∞),
所以曲线y=f(x)在点(1,f(1))处的切线斜率为f′(1)=
,
因为f(1)=
,所以曲线y=f(x)切线方程为y-
=
(x-1),
假设切线过点(2,0),代入上式得:为0-
=
(2-1),得到0=1产生矛盾,所以假设错误,
故曲线y=f(x)在点(1,f(1))处的切线不过点(2,0)…(4分)
(Ⅱ)解:由f′(x0)=0得k=
因为0<x0≤1,所以k′<0,所以k(x0)在(0,1]上单调递减,故k≥1…(7分)
(Ⅲ)证明:令g(x)=(x2+x)f′(x),当x0=1时,k=1,所以g(x)=
(1-x-xlnx),x∈(0,+∞),
因此,对任意x>0,g(x)<e-2+1等价于1-x-xlnx<
(e-2+1).…(9分)
由h(x)=1-x-xlnx,x∈(0,+∞),
所以h′(x)=-lnx-2,x∈(0,+∞),
因此,当x∈(0,e-2)时,h′(x)>0,h(x)单调递增;x∈(e-2,+∞)时,h′(x)<0,h(x)单调递减.
所以h(x)的最大值为h(e-2)=e-2+1,故1-x-xlnx≤e-2+1.…(12分)
设φ(x)=ex-(x+1),
因为φ′(x)=ex-1,所以x∈(0,+∞)时φ′(x)>0,φ(x)单调递增,φ(x)>φ(0)=0,
故x∈(0,+∞)时,φ(x)=ex-(x+1)>0,即
>1.
所以故1-x-xlnx≤e-2+1<
(e-2+1).
因此,对任意x>0,f′(x)<
恒成立 …(14分)
| lnx+k |
| ex |
| 1-kx-xlnx |
| xex |
所以曲线y=f(x)在点(1,f(1))处的切线斜率为f′(1)=
| 1-k |
| e |
因为f(1)=
| k |
| e |
| k |
| e |
| 1-k |
| e |
假设切线过点(2,0),代入上式得:为0-
| k |
| e |
| 1-k |
| e |
故曲线y=f(x)在点(1,f(1))处的切线不过点(2,0)…(4分)
(Ⅱ)解:由f′(x0)=0得k=
| 1-x0lnx0 |
| x0 |
因为0<x0≤1,所以k′<0,所以k(x0)在(0,1]上单调递减,故k≥1…(7分)
(Ⅲ)证明:令g(x)=(x2+x)f′(x),当x0=1时,k=1,所以g(x)=
| x+1 |
| ex |
因此,对任意x>0,g(x)<e-2+1等价于1-x-xlnx<
| ex |
| x+1 |
由h(x)=1-x-xlnx,x∈(0,+∞),
所以h′(x)=-lnx-2,x∈(0,+∞),
因此,当x∈(0,e-2)时,h′(x)>0,h(x)单调递增;x∈(e-2,+∞)时,h′(x)<0,h(x)单调递减.
所以h(x)的最大值为h(e-2)=e-2+1,故1-x-xlnx≤e-2+1.…(12分)
设φ(x)=ex-(x+1),
因为φ′(x)=ex-1,所以x∈(0,+∞)时φ′(x)>0,φ(x)单调递增,φ(x)>φ(0)=0,
故x∈(0,+∞)时,φ(x)=ex-(x+1)>0,即
| ex |
| x+1 |
所以故1-x-xlnx≤e-2+1<
| ex |
| x+1 |
因此,对任意x>0,f′(x)<
| e-2+1 |
| x2+x |
点评:本题考查利用导数研究曲线上某点切线方程,考查利用导数研究函数的单调性,考查不等式的证明,构造函数,确定单调性是关键.

练习册系列答案
相关题目
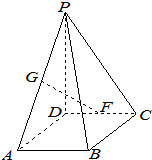 在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AB=1,BC=2,PD=
在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AB=1,BC=2,PD=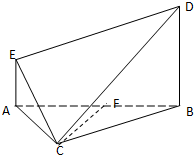 在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2
在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2