题目内容
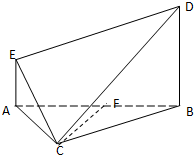 在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2
在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2(Ⅰ)求证:平面EDC⊥平面BDC;
(Ⅱ)设F为AB的中点,求直线CF与平面EDC所成角的正弦值.
考点:直线与平面所成的角,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)通过平面与平面垂直的性质定理,证明EP⊥平面BCD.
(Ⅱ)利用体积法求出F到平面DEC的距离h,再求出直线CF与平面EDC所成角的正弦值.
(Ⅱ)利用体积法求出F到平面DEC的距离h,再求出直线CF与平面EDC所成角的正弦值.
解答:
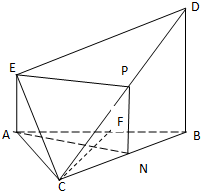 (本题满分14分)
(本题满分14分)
解、(I)取CD、CB的中点P、N,连接EP,PN,NA,则PN∥BD,且PN=
BD,∴EP∥AN…(3分)
因为,AB=BC=CA,AN⊥BC,…(4分)
因为,AE⊥平面ABC,AE∥BD,所以,平面ABC⊥平面BDC,…(6分)
∴AN⊥平面BDC,∴EP⊥平面BDC…(8分)
∴平面EDC⊥平面BDC…(9分)
(II)EC=DE=DF=
,EF=
,CF=
,DC=2
,∴S△DEC=
,S△EDF=
,…(10分)
设F到平面DEC的距离为h,由CF垂直平面ABDE和VF-EDC=VC-EDF,得h=
.…(12分)
设直线CF与平面EDC所成角为θ,则sinθ=
…(14分)
 (本题满分14分)
(本题满分14分)解、(I)取CD、CB的中点P、N,连接EP,PN,NA,则PN∥BD,且PN=
| 1 |
| 2 |
因为,AB=BC=CA,AN⊥BC,…(4分)
因为,AE⊥平面ABC,AE∥BD,所以,平面ABC⊥平面BDC,…(6分)
∴AN⊥平面BDC,∴EP⊥平面BDC…(8分)
∴平面EDC⊥平面BDC…(9分)
(II)EC=DE=DF=
| 5 |
| 2 |
| 3 |
| 2 |
| 6 |
| 3 |
| 2 |
设F到平面DEC的距离为h,由CF垂直平面ABDE和VF-EDC=VC-EDF,得h=
| 3 | ||
2
|
设直线CF与平面EDC所成角为θ,则sinθ=
| ||
| 4 |
点评:本题考查平面与平面垂直的判定,直线与平面所成角的求法,特别是利用等体积法求得F到平面DEC的距离h是关键,考查空间想象能力,逻辑推理能力,计算能力.

练习册系列答案
相关题目