题目内容
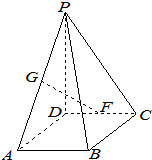 在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AB=1,BC=2,PD=
在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AB=1,BC=2,PD=| 3 |
(1)求证:AD⊥PC;
(2)求证:FG∥平面BCP.
考点:直线与平面平行的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)由已知条件推导出AD⊥CD,AD⊥PD,由此能证明AD⊥PC.
(2)取BP中点H,连接GH,CH,由此推导出四边形GFCH是平行四边形,从而能证明FG∥平面BCP.
(2)取BP中点H,连接GH,CH,由此推导出四边形GFCH是平行四边形,从而能证明FG∥平面BCP.
解答:
 (1)证明:∵底面ABCD为矩形,∴AD⊥CD,
(1)证明:∵底面ABCD为矩形,∴AD⊥CD,
∴PD⊥底面ABCD,AD?底面ABCD,∴AD⊥PD,
∵CD∩PD=D,∴AD⊥平面PDC,
∵PC?平面ABCD,∴AD⊥PC.
(2)证明:取BP中点H,连接GH,CH,
∵G,F分别为AP,DC中点,
∴GH
AB,FC
AB,
∴GH
FC,∴四边形GFCH是平行四边形,∴FG∥CH,CH?平面BCP,
FG不包含于平面BCP,∴FG∥平面BCP.
 (1)证明:∵底面ABCD为矩形,∴AD⊥CD,
(1)证明:∵底面ABCD为矩形,∴AD⊥CD,∴PD⊥底面ABCD,AD?底面ABCD,∴AD⊥PD,
∵CD∩PD=D,∴AD⊥平面PDC,
∵PC?平面ABCD,∴AD⊥PC.
(2)证明:取BP中点H,连接GH,CH,
∵G,F分别为AP,DC中点,
∴GH
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
∴GH
| ∥ |
. |
FG不包含于平面BCP,∴FG∥平面BCP.
点评:本题考查异面直线垂直的证明,考查直线与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 将数列{an}按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一个数a1,a2,a5,…构成公差为d的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为q的等比数列.若a1=1,a3=4,a5=3.
将数列{an}按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一个数a1,a2,a5,…构成公差为d的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为q的等比数列.若a1=1,a3=4,a5=3.
