题目内容

函数y=log 
1
3
（-x2+3x）的单调递减区间是
 
．
考点：复合函数的单调性
专题：函数的性质及应用
分析：令t=-x2+3x＞0，求得函数的定义域为（0，3），且y=log 
1
3
t，本题即求函数t在定义域内的增区间，
再利用二次函数的性质可得结论．
解答： 解：令t=-x2+3x＞0，求得0＜x＜3，故函数的定义域为（0，3），且y=log 
1
3
t，
故本题即求函数t在定义域内的增区间，
再利用二次函数的性质可得t=-(x-
3
2
)2在定义域（0，3）内的增区间为(0，
3
2
]，
故答案为：（0，
3
2
]．
点评：本题主要考查复合函数的单调性，对数函数、二次函数的性质，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
已知定义在R上的奇函数f（x）=
-2x+b
2x+1+a
．
（1）求a，b的值；
（2）若不等式-m2+（k+2）m-
3
2
＜f（x）＜m2+2km+k+
5
2
对一切实数x及m恒成立，求实数k的取值范围；
（3）定义：若存在一个非零常数T，使得f（x+T）=f（x）对定义域中的任何实数x都恒成立，那么，我们把f（x）叫以T为周期的周期函数，它特别有性质：对定义域中的任意x，f（x+nT）=f（x），（n∈Z）．若函数g（x）是定义在R上的周期为2的奇函数，切当x∈（-1，1）时，g（x）=f（x）-x，求方程g（x）=0的所有解．
若抛物线y2=2px的焦点与椭圆
x2
6
+
y2
2
=1的右焦点重合，则p的值为（　　）
A、-2B、2C、-4D、4
若函数f（x）=
3
sin2x+2cos2x+m在区间[0，
π
2
]上的最大值为6，求常数m的值及此函数当x∈R时的最小值，并求相应的x的取值集合．
圆锥的全面积为15πcm2，侧面展开图的中心角为60°，则圆锥的体积为
 
．
不等式（x+y-2）（x-y+1）≥0表示的平面区域时（　　）
A、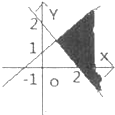
B、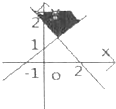
C、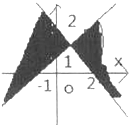
D、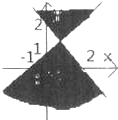
已知函数f（x）=2（m+1）x2+4mx+2m-1．
（1）若函数的一个零点在原点，①求m的值；②求当x∈[-1，2]时f（x）的值域；
（2）若0＜m＜
1
2
，求证f（x）在（0，1）上有一个零点．
解不等式：|a-2|＜|4-a2|．
在数列{an}中，a1=-2，an+1=2an+n，则a3=（　　）
A、-6B、-5C、-4D、-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网