题目内容
若抛物线y2=2px的焦点与椭圆
+
=1的右焦点重合,则p的值为( )
| x2 |
| 6 |
| y2 |
| 2 |
| A、-2 | B、2 | C、-4 | D、4 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先根据椭圆方程求出其右焦点的坐标,在于抛物线的性质可确定p的值.
解答:
解:椭圆
+
=1中,
c2=6-2=4,即c=2,
故椭圆
+
=1的右焦点为(2,0),
所以抛物线y2=2px的焦点为(2,0),
则p=4,
故选D.
| x2 |
| 6 |
| y2 |
| 2 |
c2=6-2=4,即c=2,
故椭圆
| x2 |
| 6 |
| y2 |
| 2 |
所以抛物线y2=2px的焦点为(2,0),
则p=4,
故选D.
点评:本题主要考查椭圆的简单性质和抛物线的标准方程,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
把曲线ysinx-2y+3=0先沿x轴向左平移
个单位长度,再沿y轴向下平移1个单位长度,得到曲线方程是( )
| π |
| 2 |
| A、(1-y)cosx+2y-3=0 |
| B、(1+y)sinx-2y+1=0 |
| C、(1+y)cosx-2y+1=0 |
| D、-(1+y)cosx+2y+1=0 |
设a∈Z,且0≤a<13,若512013+a能被13整除,则a=( )
| A、1 | B、2 | C、11 | D、12 |
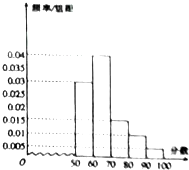 在一次物理竞赛中,学生成绩均在内[50,100),相应的频率分布直方图如图,已知成绩在[60,70)的学生有40人,则成绩在[70,90)的人数为( )
在一次物理竞赛中,学生成绩均在内[50,100),相应的频率分布直方图如图,已知成绩在[60,70)的学生有40人,则成绩在[70,90)的人数为( )