题目内容
今年双十一,淘宝网站一天的销售记录震惊全球,网购已经成为人们消费的主要形式之一.假设一淘宝网店出售某商品,根据人们的咨询量预估成交额y(千元)与售价x(千元)之间满足关系y=ax2-lnx+2(x∈(0,1))(a>
),而由于价格原因未能交易成功的成交额m(千元)与售价x(千元)之间满足关系m=x,记实际成交额为f(x).
(1)若发现该商品的实际成交额一直下降,求此时a的取值范围;
(2)证明:只要实际成交额能出现上升趋势,则实际成交额一定不会小于2(千元).
| 1 |
| 2e |
(1)若发现该商品的实际成交额一直下降,求此时a的取值范围;
(2)证明:只要实际成交额能出现上升趋势,则实际成交额一定不会小于2(千元).
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(1)求导数,该商品的实际成交额一直下降,f′(x)<0,即2ax2-x-1<0对任意x∈(0,1)恒成立,分离参数求最值,即可确定a的取值范围;
(2)由题意,f′(x)>0在x∈(0,1)上有解,设为x0,确定x=x0,函数取得极小值f(x0)=
-lnx0+2,即可证明结论.
(2)由题意,f′(x)>0在x∈(0,1)上有解,设为x0,确定x=x0,函数取得极小值f(x0)=
| 1-x0 |
| 2 |
解答:
(1)解:由题意,f(x)=ax2-lnx-x+2,则f′(x)=
,
∵该商品的实际成交额一直下降,
∴f′(x)<0,即2ax2-x-1<0对任意x∈(0,1)恒成立,
∴a<
(
+
)恒成立,
∵
∈(1,+∞),
∴
+
>2,
∴a≤1,
∴
<a≤1;
(2)证明:由题意,f′(x)>0在x∈(0,1)上有解,设为x0,∴a>1,
∴2ax02-x0-1=0,且x∈(0,x0),f′(x)<0,(x0,1),f′(x)>0,
∴x=x0,函数取得极小值f(x0)=
-lnx0+2,
∵x∈(0,1),
∴
-lnx0+2>2,
∴实际成交额一定不会小于2(千元).
| 2ax2-x-1 |
| x |
∵该商品的实际成交额一直下降,
∴f′(x)<0,即2ax2-x-1<0对任意x∈(0,1)恒成立,
∴a<
| 1 |
| 2 |
| 1 |
| x2 |
| 1 |
| x |
∵
| 1 |
| x |
∴
| 1 |
| x2 |
| 1 |
| x |
∴a≤1,
∴
| 1 |
| 2e |
(2)证明:由题意,f′(x)>0在x∈(0,1)上有解,设为x0,∴a>1,
∴2ax02-x0-1=0,且x∈(0,x0),f′(x)<0,(x0,1),f′(x)>0,
∴x=x0,函数取得极小值f(x0)=
| 1-x0 |
| 2 |
∵x∈(0,1),
∴
| 1-x0 |
| 2 |
∴实际成交额一定不会小于2(千元).
点评:本题考查利用数学知识解决实际问题,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
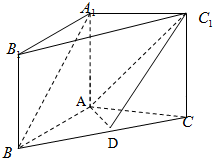 在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2
在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2