题目内容
已知抛物线y=x2-（2a-1）x+a2-1与x轴的交点为A、B．
（1）求证：点A、B在原点异侧的充要条件为-1＜a＜1；
（2）根据题意，提出一个与充分条件、必要条件、充要条件相关的问题并作出解答．
（1）求证：点A、B在原点异侧的充要条件为-1＜a＜1；
（2）根据题意，提出一个与充分条件、必要条件、充要条件相关的问题并作出解答．
考点：二次函数的性质
专题：函数的性质及应用
分析：由交点在原点的两侧得两根之积为负，解不等式求出即可．
解答：
解；（1）设A（x1，0），B（x2，0），
由题意得：x1•x2=a2-1＜0，
解得：-1＜a＜1．
（2）求证：若y=x2-（2a-1）x+a2-1与x轴有两个不同交点A，B的充要条件是a＜
，
证明：由题意得：△=（2a-1）2-4（a2-1）=5-4a＞0，
解得：a＜
．
由题意得：x1•x2=a2-1＜0，
解得：-1＜a＜1．
（2）求证：若y=x2-（2a-1）x+a2-1与x轴有两个不同交点A，B的充要条件是a＜
| 5 |
| 4 |
证明：由题意得：△=（2a-1）2-4（a2-1）=5-4a＞0，
解得：a＜
| 5 |
| 4 |
点评：本题是二次函数的性质问题，考察了一元二次方程根与系数的关系，是一道基础题．
练习册系列答案
相关题目
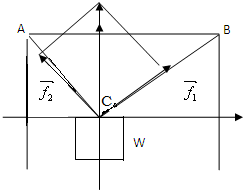物体W的质量为50千克，用绳子将物体W悬挂在两面墙之间，已知两面墙之间的距离AB=10米（AB为水平线），AC=6米，BC=8米，求AC，BC上所受的力的大小．
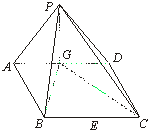如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，且∠DAB=60°．侧面PAD为正三角形，其所在的平面垂直于底面ABCD，G为AD边的中点．