题目内容
1.在平面直角坐标系xOy中,若抛物线y2=2px经过点(4,2),则实数p=$\frac{1}{2}$.分析 利用抛物线经过的点,求解即可.
解答 解:抛物线y2=2px经过点(4,2),
可得4=8P,
解得p=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查抛物线才的应用,基本知识考查.

练习册系列答案
相关题目
9.已知平面向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,m),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则|2$\overrightarrow{a}$+3$\overrightarrow{b}$|=( )
| A. | $2\sqrt{5}$ | B. | $3\sqrt{5}$ | C. | $4\sqrt{5}$ | D. | $5\sqrt{5}$ |
6.定点P(a,b)在圆x2+y2+2x=1内,直线(a+1)x+by+a-1=0与圆x2+y2+2x=1的位置关系是( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 不确定 |
2.直线$\left\{\begin{array}{l}x={x_0}+at\\ y={y_0}+bt\end{array}\right.$(t为参数)上的两个点A,B对应参数分别为t1,t2,则|AB|=( )
| A. | |t1-t2| | B. | $\sqrt{{a^2}+{b^2}}|{{t_1}-{t_2}}|$ | C. | $\frac{{|{{t_1}-{t_2}}|}}{{\sqrt{{a^2}+{b^2}}}}$ | D. | $\frac{{|{{t_1}-{t_2}}|}}{{{a^2}+{b^2}}}$ |
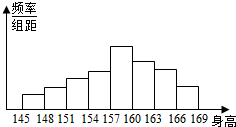 为了了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三个小组的频数为6.
为了了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三个小组的频数为6.