题目内容
已知数列{an}的前n项和为Sn,且Sn=2an-2n+1,n∈N*.设bn=log2
,tn=
+
+
+…+
,是否存在最大的正整数k,使得对于任意的正整数N,有tn>
恒成立?若存在,求出k的值,若不存在,请说明理由.
| Sn |
| n |
| 1 |
| bn |
| 1 |
| bn+1 |
| 1 |
| bn+2 |
| 1 |
| b2n-1 |
| k |
| 12 |
考点:数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:将n换成n+1,两式相减,运用n=1时,a1=S1,n>1时,an=Sn-Sn-1,即可得到数列{
}为首项为2,公差为1的等差数列,求出bn,tn,tn+1,作差,判断{tn}的单调性,求出tn的最小值,令
小于最小值,即可求出正整数k的最大值.
| an |
| 2n |
| k |
| 12 |
解答:
解:当n=1时,S1=2a1-4,解得a1=4.
由题意得Sn=2an-2n+1,Sn+1=2an+1-2n+2,
两式相减得an+1=2an+1-2an-2n+1,
于是an+1=2an+2n+1,
∴
-
=1
∴数列{
}为首项为2,公差为1的等差数列,
∴
=n+1,即an=2n(n+1)
代入Sn=n•2n+1,
∴bn=lo
=n+1,
∴tn=
+
+
+…+
=
+
+…+
,
∴tn+1-tn=
.
∵n是正整数,∴tn+1-tn>0,即tn+1>tn.
∴数列{tn}是一个单调递增数列,
又t1=b2=
,∴tn≥t1=
,
要使tn>
恒成立,则有
>
,即k<6,
又k是正整数,故存在最大正整数k=5使tn>
恒成立.
由题意得Sn=2an-2n+1,Sn+1=2an+1-2n+2,
两式相减得an+1=2an+1-2an-2n+1,
于是an+1=2an+2n+1,
∴
| an+1 |
| 2n+1 |
| an |
| 2n |
∴数列{
| an |
| 2n |
∴
| an |
| 2n |
代入Sn=n•2n+1,
∴bn=lo
| g |
2 |
∴tn=
| 1 |
| bn |
| 1 |
| bn+1 |
| 1 |
| bn+2 |
| 1 |
| b2n-1 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
∴tn+1-tn=
| 1 |
| 2(2n+1)(n+1) |
∵n是正整数,∴tn+1-tn>0,即tn+1>tn.
∴数列{tn}是一个单调递增数列,
又t1=b2=
| 1 |
| 2 |
| 1 |
| 2 |
要使tn>
| k |
| 12 |
| 1 |
| 2 |
| k |
| 12 |
又k是正整数,故存在最大正整数k=5使tn>
| k |
| 12 |
点评:本题主要考查数列的通项和求和,考查等比数列的通项,以及不等式的恒成立问题,判断数列的单调性,注意考虑相邻两项的大小,属于难题.

练习册系列答案
相关题目
函数f(x)=-x2+2x+3在区间[-2,2]上的最大、最小值分别为( )
| A、4,3 | B、3,-5 |
| C、4,-5 | D、5,-5 |
满足f(x+π)=-f(x)且为奇函数的函数f(x)可能是( )
| A、cos2x | ||
| B、sinx | ||
C、sin
| ||
| D、cosx | ||
E、sin
|
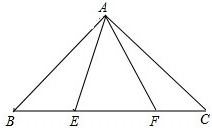 在△ABC中,AB=AC,∠BAC=90°,点E,F在BC边上(不与B,C重合),∠EAF=45°,问以BE、EF、FC三条线段为边,是否总能构成直角三角形?请说明结论及理由.
在△ABC中,AB=AC,∠BAC=90°,点E,F在BC边上(不与B,C重合),∠EAF=45°,问以BE、EF、FC三条线段为边,是否总能构成直角三角形?请说明结论及理由.