题目内容
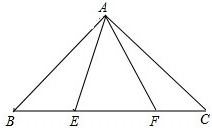 在△ABC中,AB=AC,∠BAC=90°,点E,F在BC边上(不与B,C重合),∠EAF=45°,问以BE、EF、FC三条线段为边,是否总能构成直角三角形?请说明结论及理由.
在△ABC中,AB=AC,∠BAC=90°,点E,F在BC边上(不与B,C重合),∠EAF=45°,问以BE、EF、FC三条线段为边,是否总能构成直角三角形?请说明结论及理由.考点:三角形中的几何计算
专题:综合题,立体几何
分析:将△AEB逆时针转动直至AB与AC重合,即形成的新△AE'C≌△AEB,AE'=AE,CE'=BE,连接E'F,证明△CE'F为RT△,E'F2=CE'2+FC2,即可得出结论.
解答:
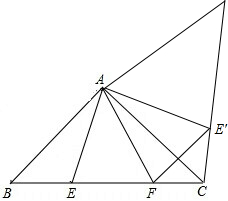 解:将△AEB逆时针转动直至AB与AC重合,即形成的新△AE'C≌△AEB,AE'=AE,CE'=BE.
解:将△AEB逆时针转动直至AB与AC重合,即形成的新△AE'C≌△AEB,AE'=AE,CE'=BE.
∠E'AC=∠EAB,∠ABE=∠ACE'=∠ACB=45°.
连接E'F.则∠E'AF=∠E'AC+∠FAC=∠EAB+∠FAC=90°-45°=45°
又∠EAF=45°,所以∠EAF=∠E'AF,
又AE'=AE,AF为公用边,
所以△E'AF≌△EAF,E'F=EF,
又∠ABE=∠ACE'=∠ACB=45°,∠ACE'+∠ACB=45°+45°=90°,
所以△CE'F为RT△,E'F2=CE'2+FC2,
又CE'=BE,E'F=EF,EF2=BE2+FC2
所以以BE,EF,FC为边的三角形是直角三角形.
 解:将△AEB逆时针转动直至AB与AC重合,即形成的新△AE'C≌△AEB,AE'=AE,CE'=BE.
解:将△AEB逆时针转动直至AB与AC重合,即形成的新△AE'C≌△AEB,AE'=AE,CE'=BE.∠E'AC=∠EAB,∠ABE=∠ACE'=∠ACB=45°.
连接E'F.则∠E'AF=∠E'AC+∠FAC=∠EAB+∠FAC=90°-45°=45°
又∠EAF=45°,所以∠EAF=∠E'AF,
又AE'=AE,AF为公用边,
所以△E'AF≌△EAF,E'F=EF,
又∠ABE=∠ACE'=∠ACB=45°,∠ACE'+∠ACB=45°+45°=90°,
所以△CE'F为RT△,E'F2=CE'2+FC2,
又CE'=BE,E'F=EF,EF2=BE2+FC2
所以以BE,EF,FC为边的三角形是直角三角形.
点评:本题考查三角形中的几何计算,考查三角形全等的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 将一块边长为a的正方形铁皮,剪去四个角(四个全等的正方形),作成一个无盖的铁盒,要使其容积最大,剪去的小正方形的边长为多少?最大容积是多少?
将一块边长为a的正方形铁皮,剪去四个角(四个全等的正方形),作成一个无盖的铁盒,要使其容积最大,剪去的小正方形的边长为多少?最大容积是多少?