Question

若平面直角坐标系中两点P与Q满足：①P、Q分别在函数f（x），g（x）的图象上；②P与Q关于点（1，1）对称，则称点对（P，Q）是一个“相望点对”（规定：（P，Q）与（Q，P）是同一个“相望点对”），函数y=

x-2

x-1

与y=2sinπx+1（-2≤x≤4）的图象中“相望点对”的个数是（　　）

• A、8
• B、6
• C、4
• D、2

Answer 1

考点：命题的真假判断与应用,函数的图象

专题：函数的性质及应用

分析：函数y=

x-2

x-1

与y=2sinπx+1（-2≤x≤4）的图象均关于（1，1）对称，根据“相望点对”的定义，可得结论．

解答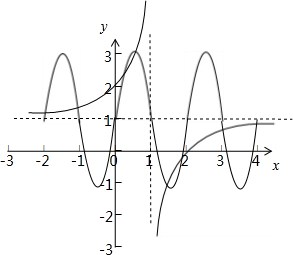： 解：由题意，函数y=

x-2

x-1

=1-

1

x-1

与y=2sinπx+1（-2≤x≤4）的图象均关于（1，1）对称，
当-2≤x≤1时，函数y=

x-2

x-1

与y=2sinπx+1的图象在（-2，0），（0，1]上分别有2个交点．
∴根据“相望点对”的定义，可得函数y=

x-2

x-1

与y=2sinπx+1（-2≤x≤4）的图象中“相望点对”的个数是4．
故选：C．

点评：本题考查新定义，考查学生分析解决问题的能力，属于中档题．