题目内容
15.若复数$\frac{(1+i)(a-i)}{i}$在复平面内对应的点位于实轴上,则|a-i|=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
分析 利用复数代数形式的乘除运算化简,再结合已知条件即可求出a的值,由复数求模公式计算得答案.
解答 解:∵$\frac{(1+i)(a-i)}{i}$=$\frac{-i(1+i)(a-i)}{-{i}^{2}}=a-1-(1+a)i$在复平面内对应的点位于实轴上,
∴-(1+a)=0,解得:a=-1.
∴|a-i|=|-1-i|=$\sqrt{(≈1)^{2}+(-1)^{2}}=\sqrt{2}$.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
相关题目
5.某几何体的三视图如图所示,则该几何体的体积为( )
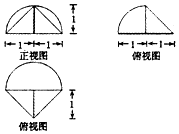

| A. | $\frac{5π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{π+1}{3}$ | D. | $\frac{2π+1}{3}$ |
6.证明1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n+1}-1}$>$\frac{n+1}{2}$(n∈N*),假设n=k时成立,当n=k+1时,左端增加的项数是( )
| A. | 2k+1项 | B. | 2k项 | C. | k+1项 | D. | k项 |
7.等差数列{an}的前n项和为Sn,已知a1-a5-a10-a15+a19=2,则S19的值为( )
| A. | 38 | B. | -19 | C. | -38 | D. | 19 |
4.设F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点,点P在双曲线上,已知|PF1|是|PF2|和|F1F2|的等差中项,且∠F1PF2=120°,则该双曲线的离心率为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
5.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4}$=1的右焦点到该双曲线渐近线的距离等于( )
| A. | 4 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2 |