��Ŀ����
3�����������ĸ����⣺����a��b��0����$\frac{1}{a}$��$\frac{1}{b}$������a��b��0����a-$\frac{1}{a}$��b-$\frac{1}{b}$������a��b��0����$\frac{2a+b}{a+2b}$��$\frac{a}{b}$����a��0��b��0��2a+b=1����$\frac{2}{a}$+$\frac{1}{b}$����СֵΪ9��������ȷ���������Ǣڢܣ�������Ϊ��ȷ�������Ŷ����ϣ���
���� ����a��b��0���ó�$\frac{1}{b}$��$\frac{1}{a}$��0���жϢٴ���
��a��b��0���ó�-$\frac{1}{a}$��-$\frac{1}{b}$���Ӷ��ó�a-$\frac{1}{a}$��b-$\frac{1}{b}$���жϢ���ȷ��
��a��b��0���ó�$\frac{2a+b}{a+2b}$-$\frac{a}{b}$��0���жϢ۴���
�������⣬���û�������ʽ�ó�$\frac{2}{a}$+$\frac{1}{b}$��9���жϢ���ȷ��
��� �⣺���ڢ٣���a��b��0����ab��0��
��$\frac{1}{ab}$��0����$\frac{1}{b}$��$\frac{1}{a}$��0���ٴ���
���ڢڣ��ɢ�֪����a��b��0����$\frac{1}{b}$��$\frac{1}{a}$��
��-$\frac{1}{b}$��-$\frac{1}{a}$����-$\frac{1}{a}$��-$\frac{1}{b}$��
��a-$\frac{1}{a}$��b-$\frac{1}{b}$������ȷ��
���ڢۣ���a��b��0����
$\frac{2a+b}{a+2b}$-$\frac{a}{b}$=$\frac{��2a+b��b-a��a+2b��}{b��a+2b��}$
=$\frac{{b}^{2}{-a}^{2}}{��a+2b��b}$
=$\frac{��b+a����b-a��}{��a+2b��b}$��0��
��$\frac{2a+b}{a+2b}$��$\frac{a}{b}$���۴���
���ڢܣ�a��0��b��0��2a+b=1����
$\frac{2}{a}$+$\frac{1}{b}$=��$\frac{2}{a}$+$\frac{1}{b}$����2a+b��
=4+1+$\frac{2b}{a}$+$\frac{2a}{b}$��5+2$\sqrt{\frac{2b}{a}•\frac{2a}{b}}$=9��
���ҽ���a=b=$\frac{1}{3}$ʱȡ�Ⱥţ������ȷ��
�ʴ�Ϊ���ڢܣ�
���� ���⿼���˲���ʽ�Ļ����������������ʽ��Ӧ�����⣬�������������������е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | {x|x=$\frac{k��}{2}$+$\frac{��}{8}$��k��Z} | B�� | {x|x=k��+$\frac{��}{8}$��k��Z} | C�� | {x|x=$\frac{k��}{2}$+$\frac{��}{4}$��k��Z} | D�� | {x|x=k��+$\frac{��}{4}$��k��Z} |
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{5��}{6}$ | D�� | $\frac{2��}{3}$ |
| A�� | 20 | B�� | 10 | C�� | 8 | D�� | 2 |
| A�� | 1 | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | $\sqrt{5}$ |
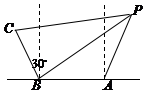 Ϊ�������㵺���丽�������������Ȩ���й��ɳ���������ɽ�š�����ʯ��ׯ�š��͡������š��ڵ��㵺�캣Ѳ����ij�գ���Ѳ����A���ġ���ɽ�š�ͻȻ��������P�������Ƶн���ij�źţ������ź�ʱ��ʯ��ׯ�š��͡������š����ֱ�λ����ͼ��ʾ��B��C����������A��B�������������6���ﴦ��C��B�ı�ƫ��30�㷽�����4���ﴦ������B��C��A��P��Զ����ˣ�4���B��C��ͬʱ������һ�źţ����źŵĴ����ٶ�Ϊÿ��1�������ȷ�����Ƶн������A�㡰��ɽ�š���λ�ã�
Ϊ�������㵺���丽�������������Ȩ���й��ɳ���������ɽ�š�����ʯ��ׯ�š��͡������š��ڵ��㵺�캣Ѳ����ij�գ���Ѳ����A���ġ���ɽ�š�ͻȻ��������P�������Ƶн���ij�źţ������ź�ʱ��ʯ��ׯ�š��͡������š����ֱ�λ����ͼ��ʾ��B��C����������A��B�������������6���ﴦ��C��B�ı�ƫ��30�㷽�����4���ﴦ������B��C��A��P��Զ����ˣ�4���B��C��ͬʱ������һ�źţ����źŵĴ����ٶ�Ϊÿ��1�������ȷ�����Ƶн������A�㡰��ɽ�š���λ�ã�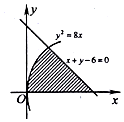 ��ͼ����������y2=8x��ֱ��x+y-6=0��x����Χ�ɵ�ͼ�Σ�ͼ����Ӱ���֣������Ϊ$\frac{40}{3}$��
��ͼ����������y2=8x��ֱ��x+y-6=0��x����Χ�ɵ�ͼ�Σ�ͼ����Ӱ���֣������Ϊ$\frac{40}{3}$��