某几何体的三视图如图所示.则该几何体的体积为( )A．$\frac{5π}{6}$B．$\frac{5π}{3}$C．$\frac{π+1}{3}$D．$\frac{2π+1}{3}$ 题目和参考答案——青夏教育精英家教网——

题目内容

5．某几何体的三视图如图所示，则该几何体的体积为（　　）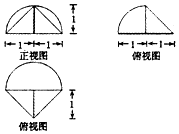

A．

$\frac{5π}{6}$

B．

$\frac{5π}{3}$

C．

$\frac{π+1}{3}$

D．

$\frac{2π+1}{3}$

分析根据题意，几何体的直观图是一个球的$\frac{1}{4}$与三棱锥的组成的几何体，利用三视图的数据，求出几何体的体积即可．

解答解：根据题意，几何体的直观图是一个球的$\frac{1}{4}$与三棱锥的组成的几何体，
则其体积V=$\frac{1}{4}$•$\frac{4π}{3}$+$\frac{1}{3}$×（$\frac{1}{2}$×2×1）×1=$\frac{π+1}{3}$；
故选：C．

点评本题考查利用三视图计算几何体的体积，关键是明确对应几何体的形状，然后利用体积公式求值．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

10．设变量x，y满足约束条件$\left\{\begin{array}{l}x-y≥0\\ 2x+y-2≤0\\ y+2≥0\end{array}\right.$，则目标函数z=|x+3y|的最大值为（　　）

16．抛掷红、蓝两颗骰子，设事件A为“蓝色骰子的点数为4或6“；事件B为“两颗骰子的点数之和大干8”求事件A发生时，事件B发生的概率是$\frac{5}{12}$．

13．已知向量$\overrightarrow{a}$=（sinx，cosx），$\overrightarrow{b}$=（sinx+cosx，sinx-cosx）（x∈R），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则x的取值集合为（　　）

{x|x=$\frac{kπ}{2}$+$\frac{π}{8}$，k∈Z}

{x|x=kπ+$\frac{π}{8}$，k∈Z}

{x|x=$\frac{kπ}{2}$+$\frac{π}{4}$，k∈Z}

{x|x=kπ+$\frac{π}{4}$，k∈Z}

20．已知复数z₁，z₂满足|z₁-$\overline{{z}_{2}}$|=|1-z₁z₂||，则有（　　）

|z₁|＜0且|z₂|＜1

|z₁|＜1或|z₂|＜1

|z₁|=1且|z₂|=1

|z₁|=1或|z₂|=1

一个长方体被一个平面截去一部分后，所剩几何体的三视图如图所示，则该几何体的体积为（　　）

17．已知方程$arctan\frac{x}{2}+arctan（2-x）=a$；
（1）若$a=\frac{π}{4}$，求$arccos\frac{x}{2}$的值；
（2）若方程有实数解，求实数a的取值范围；
（3）若方程在区间[5，15]上有两个相异的解α、β，求α+β的最大值．

14．在△ABC中，角A，B，C的对边分别为a，b，c，且c²-a²-b²=ab，则角C=（　　）

$\frac{5π}{6}$

$\frac{2π}{3}$

15．若复数$\frac{（1+i）（a-i）}{i}$在复平面内对应的点位于实轴上，则|a-i|=（　　）