题目内容
10.已知命题p:方程$\frac{x^2}{m}+\frac{y^2}{4-m}=1$表示焦点在x轴上的椭圆,命题q:(m-1)x2+(m-3)y2=1表示双曲线;若p∧q为真命题,则实数m的取值范围是2<m<3.分析 方程$\frac{x^2}{m}+\frac{y^2}{4-m}=1$表示焦点在x轴上的椭圆,则$\left\{\begin{array}{l}{m>0}\\{4-m>0}\\{m>4-m}\end{array}\right.$,从而得到p为真命题时m的范围;由:(m-1)x2+(m-3)y2=1表示双曲线得(m-1)(m-3)<0,从而得到q为真命题时m的范围.再由p∧q为真命题知p,q都是真命题,联立不等式组解出m即可.
解答 解:∵方程$\frac{x^2}{m}+\frac{y^2}{4-m}=1$表示焦点在x轴上的椭圆,
∴$\left\{\begin{array}{l}{m>0}\\{4-m>0}\\{m>4-m}\end{array}\right.$,解得2<m<4,即命题q为:2<m<4.
∵(m-1)x2+(m-3)y2=1表示双曲线,
∴(m-1)(m-3)<0,解得1<m<3,即命题q:1<m<3.
由p∧q为真命题得:p为真,q为真.
∴$\left\{\begin{array}{l}{2<m<4}\\{1<m<3}\end{array}\right.$,解得2<m<3.
故答案为:2<m<3.
点评 本题考查罗建连接词、椭圆的方程、双曲线的方程,解不等式组,属于简单题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
20.已知复数z1,z2满足|z1-$\overline{{z}_{2}}$|=|1-z1z2||,则有( )
| A. | |z1|<0且|z2|<1 | B. | |z1|<1或|z2|<1 | C. | |z1|=1且|z2|=1 | D. | |z1|=1或|z2|=1 |
5.设正实数x,y,z满足x2-3xy+4y2-z=0,则当$\frac{z}{xy}$取得最小值时,x+2y-z的最大值为( )
| A. | 1 | B. | $\frac{9}{8}$ | C. | 2 | D. | $\frac{9}{4}$ |
15.若复数$\frac{(1+i)(a-i)}{i}$在复平面内对应的点位于实轴上,则|a-i|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
19.已知复数z=$\frac{2+i}{1-2i}$,则$\overline{z}$=( )
| A. | i | B. | -i | C. | 1 | D. | -1 |
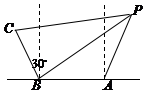 为捍卫钓鱼岛及其附属岛屿的领土主权,中国派出舰船“唐山号”、“石家庄号”和“邯郸号”在钓鱼岛领海巡航.某日,正巡逻在A处的“唐山号”突然发现来自P处的疑似敌舰的某信号,发现信号时“石家庄号”和“邯郸号”正分别位于如图所示的B、C两处,其中A在B的正东方向相距6海里处,C在B的北偏西30°方向相距4海里处.由于B、C比A距P更远,因此,4秒后B、C才同时发现这一信号(该信号的传播速度为每秒1海里),试确定疑似敌舰相对于A点“唐山号”的位置.
为捍卫钓鱼岛及其附属岛屿的领土主权,中国派出舰船“唐山号”、“石家庄号”和“邯郸号”在钓鱼岛领海巡航.某日,正巡逻在A处的“唐山号”突然发现来自P处的疑似敌舰的某信号,发现信号时“石家庄号”和“邯郸号”正分别位于如图所示的B、C两处,其中A在B的正东方向相距6海里处,C在B的北偏西30°方向相距4海里处.由于B、C比A距P更远,因此,4秒后B、C才同时发现这一信号(该信号的传播速度为每秒1海里),试确定疑似敌舰相对于A点“唐山号”的位置.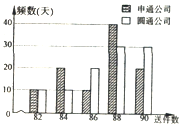 几年来,网上购物风靡,快递业迅猛发展,某市的快递业务主要由两家快递公司承接,即圆通公司与申通公司:“快递员”的工资是“底薪+送件提成”:这两家公司对“快递员”的日工资方案为:圆通公司规定快递员每天底薪为70元,每送件一次提成1元;申通公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成10元,假设同一公司的快递员每天送件数相同,现从这两家公司各随机抽取一名快递员并记录其100天的送件数,得到如下条形图:
几年来,网上购物风靡,快递业迅猛发展,某市的快递业务主要由两家快递公司承接,即圆通公司与申通公司:“快递员”的工资是“底薪+送件提成”:这两家公司对“快递员”的日工资方案为:圆通公司规定快递员每天底薪为70元,每送件一次提成1元;申通公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成10元,假设同一公司的快递员每天送件数相同,现从这两家公司各随机抽取一名快递员并记录其100天的送件数,得到如下条形图: