题目内容
定义平面向量之间的一种运算“⊙”如下:对任意向量
=(x1,y1),
=(x2,y2),令
⊙
=x1y2-x2y1,则下列说法中错误的是( )
| a |
| b |
| a |
| b |
A、2
| ||||||||
B、
| ||||||||
C、|
| ||||||||
D、若
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据定义不难得出B是错误的,x2y1-x1y2≠x1y2-x2y1,故B选项是错误的,而对于其它选项,可以分别证明它们是真命题.
解答:
解:对于选项A.2
⊙
=(2x1,2y1)⊕(x2,y2)=2x1y2-2x2y1,
⊙2
=(x1,y1)⊙(2x2,2y2)=2x1y2-2x2y1,故正确,
对于选项B.
⊙
=(x2,y2)⊙(x1,y1)=x2y1-x1y2,
⊙
=x1y2-x2y1,因为x2y1-x1y2≠x1y2-x2y1,所以
⊙
=
⊙
,故错误,
对于选项C.(|
|•|
|)2-|
⊙
|2=(x1x2+y1y2)2-(x1y2-x2y1)2=(x1x2-y1y2)2≥0.故正确,
对于选项D,若
与
共线,则x1y2-x2y1=0,由此得
⊙
=0,故正确.
故选:B.
| a |
| b |
| a |
| b |
对于选项B.
| b |
| a |
| a |
| b |
| a |
| b |
| b |
| a |
对于选项C.(|
| a |
| b |
| a |
| b |
对于选项D,若
| a |
| b |
| a |
| b |
故选:B.
点评:本题考查了在新定义下向量数量积的应用,属于基础题.牢记面向量的平行的充要条件即模长公式并准确运用它们的坐标运算,是解决本题的关键

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
已知a=log23,b=log0.53,c=4-
,则a,b,c的大小关系是( )
| 1 |
| 2 |
| A、a>c>b |
| B、a<c<b |
| C、a<b<c |
| D、a>b>c |
设O为△ABC的外心,且
+
+
=
,|
|=1则
•(
+
)值是( )
| OA |
| OB |
| 3 |
| OC |
| 0 |
| AB |
| CO |
| CA |
| CB |
A、2-
| ||
| B、2 | ||
C、2+
| ||
| D、4 |
已知|
|=4|
|≠0,且关于x的方程2x2+|
|x+
•
=0有实根,则
与
的夹角的取值范围是( )
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( )
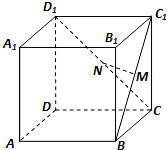

| A、MN与AB1平行 |
| B、MN与CC1垂直 |
| C、MN与AC垂直 |
| D、MN与BD平行 |
设f:A→是从A到B的一个映射,其中A=B={(x,y)|x,y∈R}.f:(x,y)→(x+y,x-y),则A中的元素(1,2)在B中的象是( )
| A、(3,-1) | ||||
B、(
| ||||
| C、(-1,3) | ||||
D、(-
|
 如图已知空间四面体D一ABC的每条边都等于1,点E,F分别是AB,AD的中点,则
如图已知空间四面体D一ABC的每条边都等于1,点E,F分别是AB,AD的中点,则