题目内容
函数y=sinx+sin(
+x)的值域是 .
| 2π |
| 3 |
考点:两角和与差的正弦函数
专题:三角函数的图像与性质
分析:由两角和与差的正弦函数公式化简函数解析式可得y=sin(x+
),由正弦函数的性质即可求值域.
| π |
| 3 |
解答:
解:∵y=sinx+sin(
+x)=sinx+
cosx-
sinx=
sinx+
cosx=sin(x+
)
∴由正弦函数的性质可知:sin(x+
)∈[-1,1],
故答案为:[-1,1].
| 2π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∴由正弦函数的性质可知:sin(x+
| π |
| 3 |
故答案为:[-1,1].
点评:本题主要考查了两角和与差的正弦函数公式的应用,考查了正弦函数的性质,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
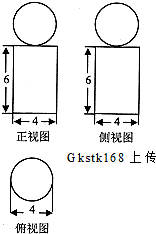 如图是一个空间几何体的三视图(注:正视图也称主视图,侧视图也称左视图),其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成,俯视图是直径等于4的圆,该几何体的体积是( )
如图是一个空间几何体的三视图(注:正视图也称主视图,侧视图也称左视图),其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成,俯视图是直径等于4的圆,该几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
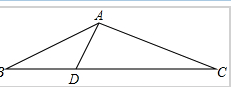 如图△ABC中,∠BAC=120°,AB=1,AC=2,D在BC上,且DC=4BD,则AD的长为
如图△ABC中,∠BAC=120°,AB=1,AC=2,D在BC上,且DC=4BD,则AD的长为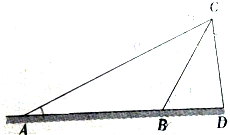 为了测量一个塔的高度,某人站在A处测得塔尖C的仰角为30°,前进100m后达到B处,测得塔尖的仰角为75°,则该塔的高度为
为了测量一个塔的高度,某人站在A处测得塔尖C的仰角为30°,前进100m后达到B处,测得塔尖的仰角为75°,则该塔的高度为