题目内容
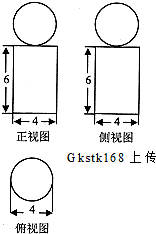如图是一个空间几何体的三视图（注：正视图也称主视图，侧视图也称左视图），其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成，俯视图是直径等于4的圆，该几何体的体积是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：由三视图求面积、体积
专题：计算题
分析：由三视图得此几何体的几何特征：上球、下圆柱，并得到球的半径、圆柱的底面半径和高，由体积公式计算出几何体的体积．
解答：
解：由三视图知几何体是一个简单组合体：上球、下圆柱组成，
且球的底面半径是2，圆柱的底面半径是2、高是6，
所以几何体的体积V=
×π×8+π×4×6=
，
故选：D．
且球的底面半径是2，圆柱的底面半径是2、高是6，
所以几何体的体积V=
| 4 |
| 3 |
| 104π |
| 3 |
故选：D．
点评：本题考查由三视图求体积，解题的关键是熟练掌握三视图的作图规则，由三视图还原出实物图的几何特征及测度．
练习册系列答案
相关题目
已知函数f（x）=
sin（ωx+φ+
）对任意的实数x，有f（-x）=f（x），则tanφ的值为（ ）
| 2 |
| π |
| 4 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
已知α，β是两个不同的平面，m，n是直线，下列命题中不正确的是（ ）
| A、若m⊥α，n⊥α，则m∥n |
| B、若m∥α，n∥α，则m∥n |
| C、若m⊥α，m⊥β，则α∥β |
| D、若m⊥α，m?β，则α⊥β |
| 3 | a |
| 3 | b |
| 3 | a-b |
| A、ab（b-a）＞0 |
| B、ab＞0且a＞b |
| C、ab＜0且a＜b |
| D、ab（b-a）＜0 |