题目内容
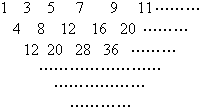 如图的倒三角形数阵满足:①第一行的第n 个数,分别是1,3,5,7,9,…,2n-1; ②从第二行起,各行中的每一个数都等于它肩上的两数之和; ③数阵共有n行;
如图的倒三角形数阵满足:①第一行的第n 个数,分别是1,3,5,7,9,…,2n-1; ②从第二行起,各行中的每一个数都等于它肩上的两数之和; ③数阵共有n行;问:第32行的第17个数是
考点:归纳推理
专题:规律型
分析:设第k行的第一个数为ak,则a1=1,a2=4=2a1+2,a3=12=2a2+22,a4=32=2a3+23,…归纳,得ak=2ak-1+2k-1(k≥2,且k∈N*),故an=n•2n-1(n∈N*).由数阵的排布规律可知,每行的数(倒数两行另行考虑)都成等差数列,且公差依次为:2,22,…,2k,…,由此能求出第32行的第17个数.
解答:
解:设第k行的第一个数为ak,
则a1=1,
a2=4=2a1+2,
a3=12=2a2+22,
a4=32=2a3+23,
…
由以上归纳,得ak=2ak-1+2k-1(k≥2,且k∈N*),
∴
=
+
,即
-
=
,
∴数列{
}是以
=
为首项,以
为公差的等差数列,
∴
=
,
∴an=n•2n-1(n∈N*).
由数阵的排布规律可知,每行的数(倒数两行另行考虑)都成等差数列,
且公差依次为:2,22,…,2k,…
第n行的首项为an=n•2n-1(n∈N*),公差为2n,
∴第32行的首项为a32=32•231=236,公差为232,
∴第32行的第17个数是236+16×232=237.
故答案为:237.
则a1=1,
a2=4=2a1+2,
a3=12=2a2+22,
a4=32=2a3+23,
…
由以上归纳,得ak=2ak-1+2k-1(k≥2,且k∈N*),
∴
| ak |
| 2k |
| ak-1 |
| 2k-1 |
| 1 |
| 2 |
| ak |
| 2k |
| ak-1 |
| 2k-1 |
| 1 |
| 2 |
∴数列{
| an |
| 2n |
| a1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| an |
| 2n |
| n |
| 2 |
∴an=n•2n-1(n∈N*).
由数阵的排布规律可知,每行的数(倒数两行另行考虑)都成等差数列,
且公差依次为:2,22,…,2k,…
第n行的首项为an=n•2n-1(n∈N*),公差为2n,
∴第32行的首项为a32=32•231=236,公差为232,
∴第32行的第17个数是236+16×232=237.
故答案为:237.
点评:本题考查数列的应用,解题时要认真审题,合理地总结规律,注意归纳法和构造法的合理运用.

练习册系列答案
相关题目
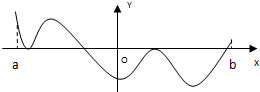 函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )
函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )| A、1个 | B、2个 | C、3个 | D、4个 |
10个三好学生名额,分给甲、乙、丙三个班,每班至少一名,共有( )种方法.
| A、24 | B、48 | C、36 | D、72 |
已知椭圆C:
+
=1(a>b>0)的左右焦点分别为F1,F2,若椭圆C上恰有8个不同的点P,使得△F1F2P为直角三角形,则椭圆C的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,
| ||||
B、(0,
| ||||
C、(
| ||||
D、[
|