题目内容
已知直线4x+3y=10和2x-y=10．
（1）直线ax+2y+8=0过两条直线的交点，求a的值；
（2）过两条直线的交点，且与直线4x-y+5=0平行的直线方程．
（1）直线ax+2y+8=0过两条直线的交点，求a的值；
（2）过两条直线的交点，且与直线4x-y+5=0平行的直线方程．
考点：直线的一般式方程与直线的垂直关系,直线的一般式方程与直线的平行关系
专题：直线与圆
分析：（1）求出直线4x+3y=10和2x-y=10的交点坐标代入直线ax+2y+8=0能求出a．
（2）设与直线4x-y+5=0平行的直线方程为4x-y+c=0，把两直线的交点代入，能求出所求直线的方程．
（2）设与直线4x-y+5=0平行的直线方程为4x-y+c=0，把两直线的交点代入，能求出所求直线的方程．
解答：
解：（1）联立
，
得直线4x+3y=10和2x-y=10的交点坐标为（4，-2），
∵直线ax+2y+8=0过两条直线的交点，
∴4a-4+8=0，解得a=-1．
（2）设与直线4x-y+5=0平行的直线方程为4x-y+c=0，
把两直线的交点（4，-2）代入，得：
16+2+c=0，解得c=-18，直线
∴所求直线的方程为4x-y-18=0．
|
得直线4x+3y=10和2x-y=10的交点坐标为（4，-2），
∵直线ax+2y+8=0过两条直线的交点，
∴4a-4+8=0，解得a=-1．
（2）设与直线4x-y+5=0平行的直线方程为4x-y+c=0，
把两直线的交点（4，-2）代入，得：
16+2+c=0，解得c=-18，直线
∴所求直线的方程为4x-y-18=0．
点评：本题考查实数的求法，考查直线方程的求法，是基础题，解题时要认真审题，注意直线与直线平行的条件的灵活运用．
练习册系列答案
优学名师名题系列答案
相关题目
为大力提倡“厉行节约，反对浪费”，某市通过随机询问100名性别不同的居民是否能做到“光盘”行动，得到如下的列联表：
下面的临界值供参考：
x2=
，其中n*1=n11+n22，n*2=n12+n21，n1*=n11+n12，n2*=n21+n22，n=n11+n22+n12+n21
下列结论正确的是（ ）
| 做不到“光盘” | 能做到“光盘” | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 25 | 20 | 45 |
| 合计 | 70 | 30 | 100 |
x2=
| n(n11n22n12n21)2 |
| n1*n2*n*1n*2 |
| P（x2≥k） | 0.05 | 0.010 | 0.005 | 0.001 |
| K | 3.841 | 6.635 | 7.879 | 10.828 |
| A、有95%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| B、有99%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| C、有99.5%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| D、性别不同决定了能否做到“光盘” |
实数x，y满足
，则3x+y的最大值为（ ）
|
A、
| ||||||
B、3+
| ||||||
C、
| ||||||
| D、17 |
圆的标准方程为：（x-a-1）2+（y-b+2）2=r2其圆心坐标是（ ）
| A、（1，-2） |
| B、（-2，1） |
| C、（a+1，b-2） |
| D、（-a-1，-b+2） |
在等比数列{an}中，a4=8a1，则公比q的值为（ ）
| A、2 | B、3 | C、4 | D、8 |
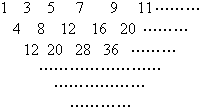如图的倒三角形数阵满足：①第一行的第n 个数，分别是1，3，5，7，9，…，2n-1； ②从第二行起，各行中的每一个数都等于它肩上的两数之和； ③数阵共有n行；