题目内容
已知椭圆C:
+
=1(a>b>0)的左右焦点分别为F1,F2,若椭圆C上恰有8个不同的点P,使得△F1F2P为直角三角形,则椭圆C的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,
| ||||
B、(0,
| ||||
C、(
| ||||
D、[
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,问题等价于椭圆上存在四个点P使得直线PF1与直线PF2垂直,可得|OP|=c>b,从而可求椭圆离心率e的取值范围.
解答:
解:由题意,问题等价于椭圆上存在四个点P使得直线PF1与直线PF2垂直,
∴|OP|=c>b,即c2>a2-c2,
∴a<
c,
∵e=
,0<e<1,
∴
<e<1
故选:C.
∴|OP|=c>b,即c2>a2-c2,
∴a<
| 2 |
∵e=
| c |
| a |
∴
| ||
| 2 |
故选:C.
点评:本题考查椭圆的几何性质,考查学生分析转化问题的能力,属于基础题,转化为椭圆上存在四个点P使得直线PF1与直线PF2垂直是关键.

练习册系列答案
相关题目
如图的程序框图,如输入x=2,则输出y为( )


| A、0 | B、-1 | C、-2 | D、-3 |
下列命题不正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若函数f(x)=ax+cos2x在区间[0,
]上是单调函数,则实数a的取值范围是( )
| π |
| 6 |
A、a≤0或a≥
| ||
B、a≥
| ||
C、a≥0或a≤-
| ||
D、a≤-
|
圆的标准方程为:(x-a-1)2+(y-b+2)2=r2其圆心坐标是( )
| A、(1,-2) |
| B、(-2,1) |
| C、(a+1,b-2) |
| D、(-a-1,-b+2) |
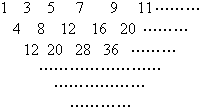 如图的倒三角形数阵满足:①第一行的第n 个数,分别是1,3,5,7,9,…,2n-1; ②从第二行起,各行中的每一个数都等于它肩上的两数之和; ③数阵共有n行;
如图的倒三角形数阵满足:①第一行的第n 个数,分别是1,3,5,7,9,…,2n-1; ②从第二行起,各行中的每一个数都等于它肩上的两数之和; ③数阵共有n行;