题目内容
10个三好学生名额，分给甲、乙、丙三个班，每班至少一名，共有（ ）种方法．
| A、24 | B、48 | C、36 | D、72 |
考点：计数原理的应用
专题：应用题,排列组合
分析：10个人站成一排，每班至少要1名，就有9个空然后插入2个板子把他们隔开，从九个里选2个即可答案．
解答：
解：10个人站成一排，每班至少要1名，就有9个空然后插入2个板子把他们隔开，从九个里选2个，就是C92=36，
故选：C．
故选：C．
点评：本题主要考查挡板法的运用，等价转化是解题的关键．
练习册系列答案
相关题目
如图是一个空间几何体的三视图，则该几何体的体积为（ ）
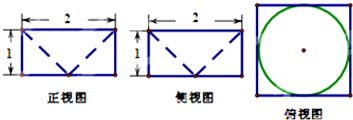
A、4-
| ||
B、8-
| ||
C、4-
| ||
D、8-
|
设函数f（x）的导函数为f′（x），对任意x∈R都有0＜f′（x）＜2成立，则（ ）
| A、f（1）＜f（3）＜f（2）+2 |
| B、f（2）+2＜f（3）＜f（1） |
| C、f（1）＜f（2）+2＜f（3） |
| D、f（2）+2＜f（1）＜f（3） |
下列命题不正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
实数x，y满足
，则3x+y的最大值为（ ）
|
A、
| ||||||
B、3+
| ||||||
C、
| ||||||
| D、17 |
若函数f（x）=ax+cos2x在区间[0，
]上是单调函数，则实数a的取值范围是（ ）
| π |
| 6 |
A、a≤0或a≥
| ||
B、a≥
| ||
C、a≥0或a≤-
| ||
D、a≤-
|
圆的标准方程为：（x-a-1）2+（y-b+2）2=r2其圆心坐标是（ ）
| A、（1，-2） |
| B、（-2，1） |
| C、（a+1，b-2） |
| D、（-a-1，-b+2） |
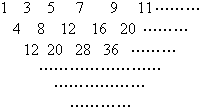如图的倒三角形数阵满足：①第一行的第n 个数，分别是1，3，5，7，9，…，2n-1； ②从第二行起，各行中的每一个数都等于它肩上的两数之和； ③数阵共有n行；