题目内容
已知函数f(x)=x2|x-a|-a,其中a>0
(1)当a=2时,求f(x)在(-∞,2)上的单调区间;
(2)讨论f(x)的零点个数.
(1)当a=2时,求f(x)在(-∞,2)上的单调区间;
(2)讨论f(x)的零点个数.
考点:利用导数研究函数的单调性,根的存在性及根的个数判断
专题:综合题,导数的综合应用
分析:(1)a=2时求出f′(x),然后在定义域内解不等式f′(x)<0,f′(x)>0即可;
(2)先去掉绝对值符号,x≥a时,由导数易判断零点个数;x<a时,通过单调性及讨论极值符号可得零点个数;
(2)先去掉绝对值符号,x≥a时,由导数易判断零点个数;x<a时,通过单调性及讨论极值符号可得零点个数;
解答:
解:(1)当a=2时,x<2,f(x)=-x3+2x2-2,f′(x)=-x(3x-4),
由f′(x)<0,得x<0或
<x<2;由f′(x)>0得0<x<
.
故 f(x)在(-∞,0)和(
,2)上单调递减,在(0,
)上单调递增;
(2)f(x)=
,
当x≥a时,f′(x)=x(3x-2a),得f(x)在(a,+∞)上单调递增,且f(a)=-a<0,
故当x≥a时有一个零点;
当x<a时,f′(x)=-x(3x-2a),得f(x)在(-∞,0)上单调递减,在(0,
)上单调递增,在(
,a)上单调递减,
∵f(0)=-a<0,∴f(x)在(-∞,0)上有一个零点;
而f(
)=
,
∴当a>
时,f(x)在(0,a)上有两个零点;
当a=
时,f(x)在(0,a)上有一个零点;
当0<a<
时,f(x)在(0,a)上无零点;
综上,当a>
时,f(x)有四个零点;当a=
时,f(x)有三个零点;当0<a<
时,f(x)有两个零点.
由f′(x)<0,得x<0或
| 4 |
| 3 |
| 4 |
| 3 |
故 f(x)在(-∞,0)和(
| 4 |
| 3 |
| 4 |
| 3 |
(2)f(x)=
|
当x≥a时,f′(x)=x(3x-2a),得f(x)在(a,+∞)上单调递增,且f(a)=-a<0,
故当x≥a时有一个零点;
当x<a时,f′(x)=-x(3x-2a),得f(x)在(-∞,0)上单调递减,在(0,
| 2a |
| 3 |
| 2a |
| 3 |
∵f(0)=-a<0,∴f(x)在(-∞,0)上有一个零点;
而f(
| 2a |
| 3 |
4a(a2-
| ||
| 27 |
∴当a>
3
| ||
| 2 |
当a=
3
| ||
| 2 |
当0<a<
3
| ||
| 2 |
综上,当a>
3
| ||
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
点评:该题考查利用导数研究函数的单调性、函数的零点,考查分类讨论思想,运用数形结合可使问题更加直观.

练习册系列答案
相关题目
设函数f(x)的导函数为f′(x),对任意x∈R都有0<f′(x)<2成立,则( )
| A、f(1)<f(3)<f(2)+2 |
| B、f(2)+2<f(3)<f(1) |
| C、f(1)<f(2)+2<f(3) |
| D、f(2)+2<f(1)<f(3) |
圆的标准方程为:(x-a-1)2+(y-b+2)2=r2其圆心坐标是( )
| A、(1,-2) |
| B、(-2,1) |
| C、(a+1,b-2) |
| D、(-a-1,-b+2) |
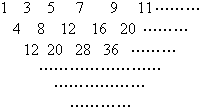 如图的倒三角形数阵满足:①第一行的第n 个数,分别是1,3,5,7,9,…,2n-1; ②从第二行起,各行中的每一个数都等于它肩上的两数之和; ③数阵共有n行;
如图的倒三角形数阵满足:①第一行的第n 个数,分别是1,3,5,7,9,…,2n-1; ②从第二行起,各行中的每一个数都等于它肩上的两数之和; ③数阵共有n行;