题目内容
不等式log
（x2+1）＜-1的解集为 ．
| 1 |
| 2 |
考点：指、对数不等式的解法
专题：函数的性质及应用
分析：考查对数函数y=log
t的单调性，根据题意，列出不等式（组），求出x的取值范围即可．
| 1 |
| 2 |
解答：
解：∵log
（x2+1）＜-1，
∴x2+1＞2，
即x2＞1；
解得x＞1或x＜-1；
∴不等式的解集为（-∞，-1）∪（1，+∞）．
故答案为：（-∞，-1）∪（1，+∞）．
| 1 |
| 2 |
∴x2+1＞2，
即x2＞1；
解得x＞1或x＜-1；
∴不等式的解集为（-∞，-1）∪（1，+∞）．
故答案为：（-∞，-1）∪（1，+∞）．
点评：本题考查了对数不等式的解法问题，解题时应根据题意，结合对数函数的单调性，列出不等式（组），求解即可，是基础题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
下列命题不正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
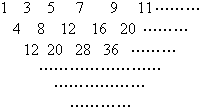如图的倒三角形数阵满足：①第一行的第n 个数，分别是1，3，5，7，9，…，2n-1； ②从第二行起，各行中的每一个数都等于它肩上的两数之和； ③数阵共有n行；