题目内容
已知y=
,求y的最大值.
| 1+sinx |
| 2+cosx |
考点:三角函数的最值
专题:计算题,函数的性质及应用,三角函数的图像与性质
分析:法一:去分母,原式化为sinx-ycosx=2y-1,即sin(x-φ)=
.利用正弦函数的有界性即可求解;
法二:令x1=-cosx,y1=-sinx,有x12+y12=1.它表示单位圆,则所给函数y就是经过定点P(2,1)以及该圆上的动点M(-cosx,-sinx)的直线PM的斜率k,故只需求此直线的斜率k的最值即可.
| 2y-1 | ||
|
法二:令x1=-cosx,y1=-sinx,有x12+y12=1.它表示单位圆,则所给函数y就是经过定点P(2,1)以及该圆上的动点M(-cosx,-sinx)的直线PM的斜率k,故只需求此直线的斜率k的最值即可.
解答:
解法一:去分母,原式化为
sinx-ycosx=2y-1,
即sin(x-φ)=
.
故
≤1,解得0≤y≤
.
则ymax=
;
解法二:令x1=-cosx,y1=-sinx,有x12+y12=1.
它表示单位圆,则所给函数y就是经过定点P(2,1)
以及该圆上的动点M(-cosx,-sinx)的直线PM的斜率k,
故只需求此直线的斜率k的最值即可.由
=1,得k=0或
.
则ymax=
.
sinx-ycosx=2y-1,
即sin(x-φ)=
| 2y-1 | ||
|
故
| |2y-1| | ||
|
| 4 |
| 3 |
则ymax=
| 4 |
| 3 |
解法二:令x1=-cosx,y1=-sinx,有x12+y12=1.
它表示单位圆,则所给函数y就是经过定点P(2,1)
以及该圆上的动点M(-cosx,-sinx)的直线PM的斜率k,
故只需求此直线的斜率k的最值即可.由
| |1-2k| | ||
|
| 4 |
| 3 |
则ymax=
| 4 |
| 3 |
点评:本题考查了函数的最值的求法,考查三角函数的最值,注意运用辅助角公式和正弦函数的值域,以及直线的斜率的运用,与直线和圆相切的条件,属于中档题.

练习册系列答案
相关题目
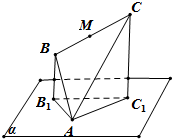 如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,M为BC的中点.若△ABC在平面α上的射影是以A为直角顶点的三角形AB1C1,则M到平面α的距离的取值范围是
如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,M为BC的中点.若△ABC在平面α上的射影是以A为直角顶点的三角形AB1C1,则M到平面α的距离的取值范围是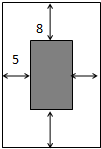 如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?