题目内容
（1）计算：
；
（2）根据（1）写出行列式的性质并加以证明．
|
（2）根据（1）写出行列式的性质并加以证明．
考点：三阶矩阵
专题：矩阵和变换
分析：（1）由行列式的计算方法解得即可；
（2）性质：若行列式中有两行完全相同，则这个行列式的值为零，由行列式的计算方法即可得出结论．
（2）性质：若行列式中有两行完全相同，则这个行列式的值为零，由行列式的计算方法即可得出结论．
解答：
解：（1）
=（1×3×9+1×3×4+1×3×7）-（1×3×4+3×7×1+9×1×3）=0
（2）性质：若行列式中有两行完全相同，则这个行列式的值为零．
证明：根据行列式的定义和性质可得，一行减去另一行的倍数，行列式值不变，所以可以得到一个全0行，
而计算行列式时候，需要每行出一个数字，所以，故必然为0．
|
（2）性质：若行列式中有两行完全相同，则这个行列式的值为零．
证明：根据行列式的定义和性质可得，一行减去另一行的倍数，行列式值不变，所以可以得到一个全0行，
而计算行列式时候，需要每行出一个数字，所以，故必然为0．
点评：本题主要考查行列式的计算及性质，属于基础题．
练习册系列答案
相关题目
已知函数f（x）在[0，+∞）上可导，其导函数记作f′（x），f（0）=-2，且f（x+π）=
f（x），当x∈[0，π）时，f′（x）•cos2x＞f（x）•sin2x-f′（x），若方程f（x）+knsecx=0在[0，+∞）上有n个解，则数列{
}的前n项和为（ ）
| 1 |
| 2 |
| n |
| k2n |
| A、（n-1）•2n+1 | ||
| B、（n-1）•2n+1+2 | ||
| C、n•2n-1 | ||
D、
|
函数f（x）=
的定义域为（ ）
| x2-9 |
| A、[-3，3] |
| B、（-3，3） |
| C、（-∞，-3]∪[3，+∞） |
| D、（-∞，-3）∪（3，+∞） |
设Sn为数列{an}的前n项和，an=1+2+22+…+2n-1，则Sn的值为（ ）
| A、2n-1 |
| B、2n-1-1 |
| C、2n-n-2 |
| D、2n+1-n-2 |
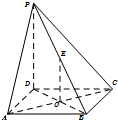如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是正方形，AC与BD交于点O，E为PB的中点．