题目内容
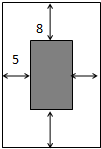 如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
如图设计一幅矩形宣传画,要求画面(阴影部分)面积为4840cm2,画面上下边要留8cm空白,左右要留5cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?考点:基本不等式在最值问题中的应用,函数模型的选择与应用
专题:函数的性质及应用,不等式的解法及应用
分析:设画面高为xcm,宽为ycm,求出所需纸张面积S的表达式,利用基本不等式求解即可.
解答:
解:设画面高为xcm,宽为ycm,依意有xy=4840,x>0,y>0--------(2分)
则所需纸张面积S=(x+16)(y+10)=xy+16y+10x+160,
即S=5000+16y+10x,--------(4分)
∵x>0,y>0,xy=4840
∴16y+10x≥2
=2
=6760-----------(8分)
当且仅当16y=10x,即x=88,y=55时等号成立.----------(9分)
即当画面高为88cm,宽为55cm时,所需纸张面积最小为6760cm2--------(10分)
则所需纸张面积S=(x+16)(y+10)=xy+16y+10x+160,
即S=5000+16y+10x,--------(4分)
∵x>0,y>0,xy=4840
∴16y+10x≥2
| 160xy |
| 160×4840 |
当且仅当16y=10x,即x=88,y=55时等号成立.----------(9分)
即当画面高为88cm,宽为55cm时,所需纸张面积最小为6760cm2--------(10分)
点评:本题考查函数的模型与应用,基本不等式的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
有一个几何体的三视图如图所示,这个几何体应该是一个( )


| A、圆台 | B、圆锥 | C、圆柱 | D、都不对 |
若函数y=ax-(b+1)(a>0,a≠1)的图象在第一、三、四象限,则有( )
| A、a>1且b<1 |
| B、a>1且b>0 |
| C、0<a<1且b>0 |
| D、0<a<1且b<0 |
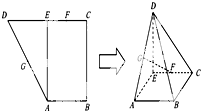 如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.
如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.