题目内容
设函数f（x）是f1（x）=4x+1，f2（x）=x+2，f3（x）=-2x+4三个函数的最小值，则f（x）的最大值为 ．
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：先在同一直角坐标系中画出三条直线，再在不同区间上取靠下的函数图象，组成f（x）的图象，由图象即可看出函数的最大值，通过解直线方程即可得此最值
解答：
解：由题意，可得函数f（x）的图象如图：
由
得A（
，
）
∴f（x）的最大值为
故答案为：
．
由
|
| 2 |
| 3 |
| 3 |
| 8 |
∴f（x）的最大值为
| 8 |
| 3 |
故答案为：
| 8 |
| 3 |
点评：本题主要考查了利用函数图象数形结合求函数最值的方法，理解新定义函数的意义，并能画出其图象是解决问题的关键
练习册系列答案
相关题目
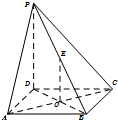如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是正方形，AC与BD交于点O，E为PB的中点．
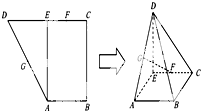如图，已知直角梯形ABCD中，E为CD边中点，且AE⊥CD，又G，F分别为DA，EC的中点，将△ADE沿AE折叠，使得DE⊥EC．有一个几何体的三视图如图所示，这个几何体应该是一个（ ）
| A、圆台 | B、圆锥 | C、圆柱 | D、都不对 |