题目内容
已知函数f(x)=xlnx,g(x)=-x2+ax-3,
(Ⅰ)求函数f(x)的单调区间和最小值;
(Ⅱ)若对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.
(Ⅰ)求函数f(x)的单调区间和最小值;
(Ⅱ)若对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(Ⅰ)由f(x)=xlnx,知f′(x)=1+lnx,利用导数的正负,可得函数f(x)的单调区间,从而可求函数的最小值;
(Ⅱ)由对一切x∈(0,+∞),2f(x)≥g(x)恒成立,知2xlnx≥-x2+ax-3,分离参数,求最值,由此能够求出实数a的取值范围.
(Ⅱ)由对一切x∈(0,+∞),2f(x)≥g(x)恒成立,知2xlnx≥-x2+ax-3,分离参数,求最值,由此能够求出实数a的取值范围.
解答:
解:(Ⅰ)∵f(x)=xlnx,
∴f′(x)=1+lnx,x>0,
由f′(x)=1+lnx<0,可得0<x<
,f′(x)=1+lnx>0,可得x>
,
∴函数f(x)的减区间为(0,
),增区间为(
,+∞).
∴x=
时,函数取得最小值-
;
(Ⅱ)∵对一切x∈(0,+∞),2f(x)≥g(x)恒成立,
∴2xlnx≥-x2+ax-3,
∴a≤2lnx+x+
,
令h(x)=2lnx+x+
,
则h′(x)=
当x>1时,h(x)是增函数,
当0<x<1时,h(x)是减函数,
∴a≤h(1)=4.
即实数a的取值范围是(-∞,4].
∴f′(x)=1+lnx,x>0,
由f′(x)=1+lnx<0,可得0<x<
| 1 |
| e |
| 1 |
| e |
∴函数f(x)的减区间为(0,
| 1 |
| e |
| 1 |
| e |
∴x=
| 1 |
| e |
| 1 |
| e |
(Ⅱ)∵对一切x∈(0,+∞),2f(x)≥g(x)恒成立,
∴2xlnx≥-x2+ax-3,
∴a≤2lnx+x+
| 3 |
| x |
令h(x)=2lnx+x+
| 3 |
| x |
则h′(x)=
| (x+3)(x-1) |
| x2 |
当x>1时,h(x)是增函数,
当0<x<1时,h(x)是减函数,
∴a≤h(1)=4.
即实数a的取值范围是(-∞,4].
点评:本题考查利用导数求函数的单调区间和实数的取值范围的方法,解题时要认真审题,仔细解答,注意分类讨论思想和等价转化思想的合理运用.

练习册系列答案
相关题目
 如图,△ABC内接于圆O,∠A的平分线交BC于点D,交外接圆于点E,求证:AD2=AB•AC-BD•DC.
如图,△ABC内接于圆O,∠A的平分线交BC于点D,交外接圆于点E,求证:AD2=AB•AC-BD•DC.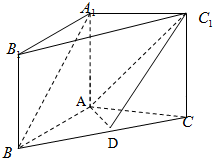 在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2
在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2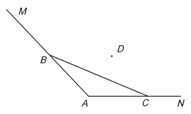 在一个六角形体育馆的一角MAN内,用长为a的围栏设置一个运动器材储存区域(如图所示),已知∠A=120°,B是墙角线AM上的一点,C是墙角线AN上的一点.
在一个六角形体育馆的一角MAN内,用长为a的围栏设置一个运动器材储存区域(如图所示),已知∠A=120°,B是墙角线AM上的一点,C是墙角线AN上的一点.