题目内容
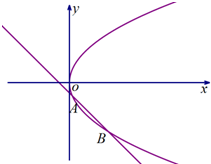 已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.
已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.(Ⅰ)若以AB为直径的圆与x轴相切,求该圆的方程;
(Ⅱ)若直线l与y轴负半轴相交,记△AOB面积为S,求
| S | ||
|
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)令线段AB中点坐标为P(x0,y0),由已知条件推导出|y0|=
,椭圆弦长公式推导出2
=2,由此能求出圆的方程.
(Ⅱ)由(Ⅰ)知,|AB|=4
,点O到直线AB的距离d=
,由此能求出
的最大值.
| |AB| |
| 2 |
| 2 |
| 1+b |
(Ⅱ)由(Ⅰ)知,|AB|=4
| 2 |
| 1+b |
| |b| | ||
|
| S | ||
|
解答:
解:(Ⅰ)令线段AB中点坐标为P(x0,y0),
∵以AB为直径的圆与x轴相切,∴|y0|=
,
由y2=4x,y=-x+b,得y2+4y-4b=0,
由△=16+16b>0,得b>-1,
y1+y2=-4,y1•y2=-4b,x1+x2=2b-(y1+y2),
∴|AB|=
=
=
=
=4
y0=
=-2,
∴2
=2,
解得b=-
,
∴所求圆的方程为(x-
)2+(y+2)2=4.( 8分)
(Ⅱ)由(Ⅰ)知,|AB|=4
,
点O到直线AB的距离d=
,S=
×4
×
=2
|b|,
=2
=2
,
∵-1<b<0,∴当b=-
时,
取最大值1.(15分)
∵以AB为直径的圆与x轴相切,∴|y0|=
| |AB| |
| 2 |
由y2=4x,y=-x+b,得y2+4y-4b=0,
由△=16+16b>0,得b>-1,
y1+y2=-4,y1•y2=-4b,x1+x2=2b-(y1+y2),
∴|AB|=
| (x1-x2)2+(y1-y2)2 |
| 2 |
| (y1-y2)2 |
| 2 |
| (y1+y2)2-4y1y2 |
=
| 2 |
| 16+16b |
| 2 |
| 1+b |
| y1+y2 |
| 2 |
∴2
| 2 |
| 1+b |
解得b=-
| 1 |
| 2 |
|

∴所求圆的方程为(x-
| 3 |
| 2 |
(Ⅱ)由(Ⅰ)知,|AB|=4
| 2 |
| 1+b |
点O到直线AB的距离d=
| |b| | ||
|
| 1 |
| 2 |
| 2 |
| 1+b |
| |b| | ||
|
| 1+b |
| S | ||
|
| (1+b)(-b) |
-(b+
|
∵-1<b<0,∴当b=-
| 1 |
| 2 |
| S | ||
|
点评:本题考查圆的方程的求法,考查
的最大值的求法,解题时要认真审题,注意椭圆的弦长公式的合理运用.
| S | ||
|

练习册系列答案
相关题目
已知集合A={x|(
)x<1},B={x|x2-3x-4>0},则A∩B等于( )
| 1 |
| 2 |
| A、{x|x>0} |
| B、{x|x<-1或x>0} |
| C、{x|x>4} |
| D、{x|-1≤x≤4} |
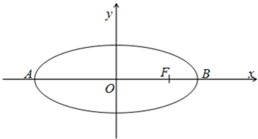 在平面直角坐标系xoy中,如图,已知椭圆
在平面直角坐标系xoy中,如图,已知椭圆