题目内容
已知函数f(x)=aln(x+1),g(x)=x-
x2,a∈R.
(1)若a=-1,求曲线y=f(x)在x=0处的切线方程;
(2)若对任意的x∈[0,+∞),都有f(x)≥g(x)恒成立,求a的最小值;
(3)设p(x)=f(x-1),a>0,若A(x1,y1),B(x2,y2)为曲线y=p(x)的两个不同点,满足0<x1<x2,且?x3∈(x1,x2),使得曲线y=P(x)在(x3,P(x3))处的切线与直线AB平行,求证:x3<
.
| 1 |
| 2 |
(1)若a=-1,求曲线y=f(x)在x=0处的切线方程;
(2)若对任意的x∈[0,+∞),都有f(x)≥g(x)恒成立,求a的最小值;
(3)设p(x)=f(x-1),a>0,若A(x1,y1),B(x2,y2)为曲线y=p(x)的两个不同点,满足0<x1<x2,且?x3∈(x1,x2),使得曲线y=P(x)在(x3,P(x3))处的切线与直线AB平行,求证:x3<
| x1+x2 |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)将a=-1代入f(x)=aln(x+1),然后求出f(x)在x=0处的导数值即为切线方程的斜率,从而可得到切线方程.
(2)根据f(x)≥g(x)恒成立,即aln(x+1)-x+
x2≥0恒成立.令h(x)=aln(x+1)-x+
x2,x≥0.根据h(x)的导数研究函数h(x)的单调性,从而求出a的最小值.
(3)p(x)=f(x-1)=alnx,欲证x3<
?证明p′(x3)<p′(
).变形可得,ln
>
=
.构造函数q(t)=lnt+
-1,t>1,利用导数求其最小值,确定q(t)>q(1)=0,即可证出结论.
(2)根据f(x)≥g(x)恒成立,即aln(x+1)-x+
| 1 |
| 2 |
| 1 |
| 2 |
(3)p(x)=f(x-1)=alnx,欲证x3<
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x2 |
| x1 |
| 2(x2-x1) |
| x1+x2 |
2(
| ||
1+
|
| 1 |
| t |
解答:
解:(1)∵a=-1,
∴f(x)=-ln(x+1).
∴f(0)=0.
∴f′(x)=-
.
∴f′(0)=-1.
∴曲线y=f(x)在x=0处的切线方程为x+y=0.
(2)f(x)≥g(x)恒成立,
即aln(x+1)≥x-
x2(a∈R)恒成立.
即aln(x+1)-x+
x2≥0恒成立.
令h(x)=aln(x+1)-x+
x2,x≥0.
则h′(x)=
-1+x=
,x≥0.
(Ⅰ)若a≥1,
则h′(x)≥0恒成立.
∴函数h(x)=在[0,+∞)上位单调递增函数.
∴h(x)≥h(0)恒成立.
又∵h(0)=0,
∴a≥1符合条件.
(Ⅱ)若a<1,
则由h′(x)=0,得x2=1-a.
解得,x=
或x=-
(舍去).
当x∈[0,
)时,h′(x)<0.
当x∈[
,+∞)时,h′(x)>0.
∴h(x)极小值=h(
).
∴h(
)<h(0)=0.
这与h(x)≥0恒成立矛盾.
综上,a≥1.
∴a的最小值为1.
(3)p(x)=f(x-1)=alnx,
则kAB=
.
又∵p′(x)=
,
∴p′(x3)=
.
∴
=
.
由p′(x)=
,a>0.易知其在定义域内为单调递减函数.
∴欲证x3<
?证明p′(x3)<p′(
).
即
>
.
变形可得,
ln
>
=
.
令
=t,t>1.
原不等式等价于lnt>
,
即(t+1)lnt>2(t-1).
构造函数q(t)=lnt+
-1,t>1.
当t>1时,q′(t)=
-
=
>0.
∴q′(t)在(1,+∞)上为单调递增函数.
∴q′(t)>q′(1)=0.
∴q(t)在为单调递增函数
∴q(t)>q(1)=0.
∴q(t)>0在(1,+∞)上恒成立.
∴(t+1)lnt>2(t-1)成立.
∴x3<
得证.
∴f(x)=-ln(x+1).
∴f(0)=0.
∴f′(x)=-
| 1 |
| x+1 |
∴f′(0)=-1.
∴曲线y=f(x)在x=0处的切线方程为x+y=0.
(2)f(x)≥g(x)恒成立,
即aln(x+1)≥x-
| 1 |
| 2 |
即aln(x+1)-x+
| 1 |
| 2 |
令h(x)=aln(x+1)-x+
| 1 |
| 2 |
则h′(x)=
| a |
| x+1 |
| x2+a-1 |
| x+1 |
(Ⅰ)若a≥1,
则h′(x)≥0恒成立.
∴函数h(x)=在[0,+∞)上位单调递增函数.
∴h(x)≥h(0)恒成立.
又∵h(0)=0,
∴a≥1符合条件.
(Ⅱ)若a<1,
则由h′(x)=0,得x2=1-a.
解得,x=
| 1-a |
| 1-a |
当x∈[0,
| 1-a |
当x∈[
| 1-a |
∴h(x)极小值=h(
| 1-a |
∴h(
| 1-a |
这与h(x)≥0恒成立矛盾.
综上,a≥1.
∴a的最小值为1.
(3)p(x)=f(x-1)=alnx,
则kAB=
| alnx2-alnx1 |
| x2-x1 |
又∵p′(x)=
| a |
| x |
∴p′(x3)=
| a |
| x3 |
∴
| alnx2-alnx1 |
| x2-x1 |
| a |
| x3 |
由p′(x)=
| a |
| x |
∴欲证x3<
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
即
| alnx2-alnx1 |
| x2-x1 |
| 2a |
| x1+x2 |
变形可得,
ln
| x2 |
| x1 |
| 2(x2-x1) |
| x1+x2 |
2(
| ||
1+
|
令
| x2 |
| x1 |
原不等式等价于lnt>
| 2(t-1) |
| t+1 |
即(t+1)lnt>2(t-1).
构造函数q(t)=lnt+
| 1 |
| t |
当t>1时,q′(t)=
| 1 |
| t |
| 1 |
| t2 |
| t-1 |
| t2 |
∴q′(t)在(1,+∞)上为单调递增函数.
∴q′(t)>q′(1)=0.
∴q(t)在为单调递增函数
∴q(t)>q(1)=0.
∴q(t)>0在(1,+∞)上恒成立.
∴(t+1)lnt>2(t-1)成立.
∴x3<
| x1+x2 |
| 2 |
点评:本题考查利用导数研究函数的单调性及极值和最值等知识的综合应用,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
执行如图所示的程序框图,输出的M的值是( )


| A、2 | ||
| B、-1 | ||
C、
| ||
| D、-2 |
已知α∈(
,π),且tan(α+
)=-
,则sinα+cosα的值是( )
| π |
| 2 |
| π |
| 4 |
| 1 |
| 7 |
A、
| ||
B、-
| ||
C、-
| ||
D、-
|
已知点P为三棱锥O-ABC的底面ABC所在平面内的一点,且
=
+k
-
,则实数k的值为( )
| OP |
| 1 |
| 2 |
| OA |
| OB |
| OC |
A、-
| ||
B、
| ||
| C、1 | ||
D、
|
 某几何体的三视图如图所示,其俯视图是中心角为60°的扇形,则该几何体的体积为
某几何体的三视图如图所示,其俯视图是中心角为60°的扇形,则该几何体的体积为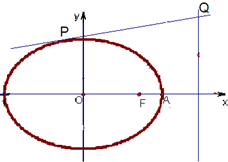 已知椭圆C:
已知椭圆C: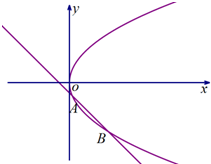 已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.
已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.